LeetCode 11 Container With Most Water（最大水容器）

LeetCode 11 Container With Most Water（最大水容器）

翻譯

給定n個非負整數a1,a2,...,an，其中每個代表一個點坐標（i,ai）。

n個垂直線段例如線段的兩個端點在（i,ai）和（i,0）。

找到兩個線段，與x軸形成一個容器，使其包含最多的水。

備注：你不必傾倒容器。

翻譯

Given n non-negative integers a1, a2, ..., an, 
where each represents a point at coordinate (i, ai). 

n vertical lines are drawn 
such that the two endpoints of line i is at (i, ai) and (i, 0). 

Find two lines, which together with x-axis forms a container, 
such that the container contains the most water.

Note: You may not slant the container.

題目的意思是，數組中的每個數對應一條線段的長度，索引對應x坐標，兩個索引可以組成一個底部的寬，高度就是前面所說的線段的長度，而既然是要盛水，高度就是兩個線段中較短的一個。

那麼該怎麼去解題呢？

你水平不行，英文也不行，所以每次一開始都是用最簡單的方法，旨在試試有沒有理解題目的意思，即便超出時間/空間限制也沒事。

public int MaxAera(int[] height)
{
    int area = 0;
    for (int i = 0; i < height.Length; i++)
    {
        for (int j = i + 1; j < height.Length; j++)
        {
            if (height[i] < height[j])
                area = Math.Max(area, countArea(height, i, j));
        }
    }
    return area;
}

public int countArea(int[] height, int x, int y)
{
    int h = height[x] > height[y] ? height[x] : height[y];
    int info = h * (y - x);
    return info;
}

很明顯這樣是不行的……

那有那些部分可以簡化呢？

前面的方法是從數組左側開始逐個向右遍歷所有情況，但明顯可以從兩側向中間進發，通過對應的max函數來保留最大的面積。

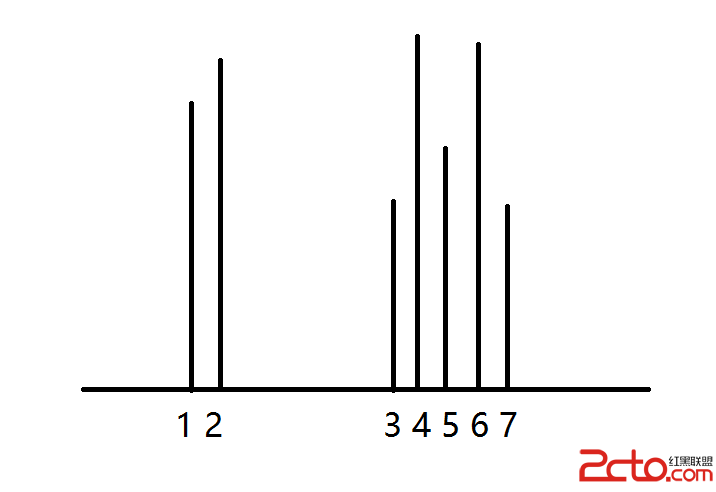
當從左邊進入到圖中線段1位置，右邊進入到線段5的時候。你不會想著右邊繼續進入線段6和7，因為你就是從那邊過來的。

那麼是該左邊的往右走，還是右邊的往左走呢？

如果是右邊的往左走，雖然線段1變成了線段2，但是線段1到線段5的距離比線段2大，因此面積也大。所以走了之後面積反而小了。

如果是右邊的往左走，親自行腦補：線段3和線段4是在同一位置，如果是到了線段4，那麼容器的高度將從原本的線段5的長度變成線段1的長度，（雖然由於距離的變小，總面積仍可能變小，但請繼續往下看），而如果到了線段3，雖然高度變小了，寬度變小了，但，那又何妨呢？因為你的maxArea還是在那裡的，每次的計算後，當且僅當高度超過原本的高度之後才會覆蓋原來的值。

maxArea = Max(maxArea,newArea);

也就是說，高度如果沒有超過，就沒有什麼影響。

至於你說它會不會因為自增和自減而發生越界，如果

int[] height = {10, 1, 2, 3, 4, 5, 6, 7, 11};

假設這裡的10和11對應線段1和線段6，請自行腦補：去掉線段7，既然線段1短於線段6，那麼發生的是left++，而不是left–。所以，並不會越界的。反之，亦然。

public class Solution
{
    public int MaxArea(int[] height)
    {
        int left = 0, right = height.Length - 1;
        int maxArea = 0;
        while (left < right && left >= 0 && right <= height.Length - 1)
        {
            maxArea = Math.Max(maxArea, Math.Min(height[left], height[right]) * (right - left));
            if (height[left] > height[right])
            {
                right--;
            }
            else
            {
                left++;
            }
        }
        return maxArea;
    }
}

明天繼續，加油！