本文是對http://noalgo.info/476.html的一點理解,特別是對其中
int father[mx]; //節點的父親 int ancestor[mx]; //已訪問節點集合的祖先
這兩個數組作用的解釋;
首先必須明確,並查集重建的樹跟原來的樹並不一樣;
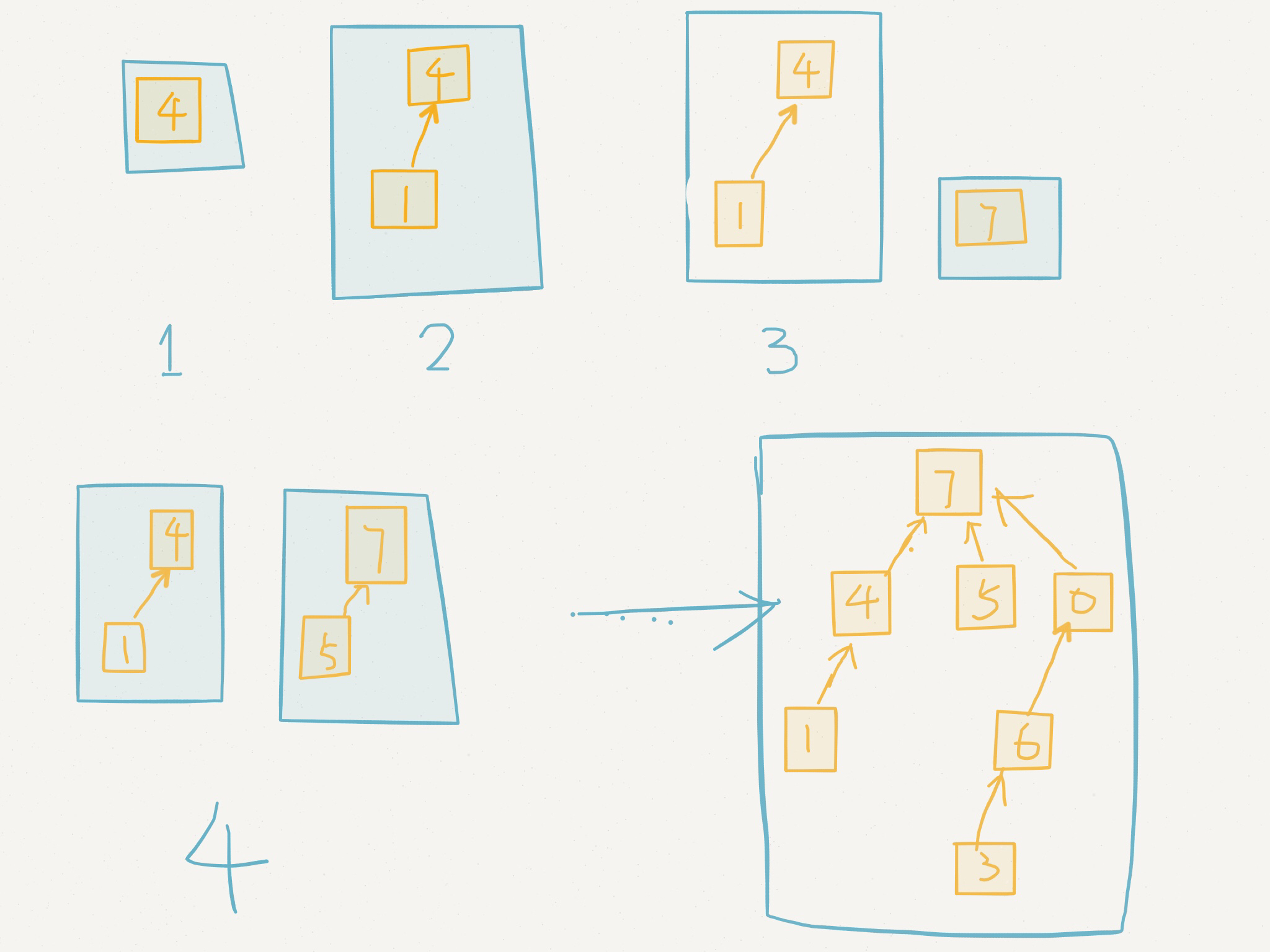
還是借用該文章的例子:
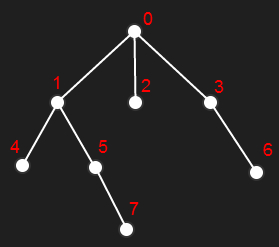
Tarjan算法是基於DFS(深度優先搜索), 圖中的樹深度優先遍歷的順序應該是:
4->7->5->1->2->6->3->0
但作者卻說,節點的處理順序為:
4->7->5->1->0->2->6->3
其實, 這裡第一種順序是我們處理查詢請求的順序,例如我們遍歷到5, 則我們可以獲得 5與5之前的所有已經遍歷過的節點即(5,4) (5,7)的查詢結果;
第二種順序則是我們建立並查集的順序
關鍵代碼如下:
1 void Tarjan(int x) //Tarjan算法求解LCA
2 {
3 for (int i = 0; i < tree[x].size(); i++)
4 {
5 Tarjan(tree[x][i]); //訪問子樹
6 unionSet(x, tree[x][i]); //將子樹節點與根節點x的集合合並,這裡是並查集處理節點x
7 ancestor[findSet(x)] = x;//合並後的集合的祖先為x
8 }
9 vs[x] = 1; //標記為已訪問, 這裡是DFS遍歷節點x
10 for (int i = 0; i < query[x].size(); i++) //與根節點x有關的查詢
11 if (vs[query[x][i]]) //如果查詢的另一個節點已訪問,則輸出結果
12 printf("%d和%d的最近公共祖先為:%d\n", x,
13 query[x][i], ancestor[findSet(query[x][i])]);
14 }
兩者順序不同的原因在於下面的第6行和第9行代碼,我們在還未遍歷父節點的時候,處理第一個子樹後,父節點就已經在並查集內了;例如我們還沒有遍歷節點1,在遍歷節點4後,就會處理節點4與其父節點1的合並;
下面,我們來慢慢建立並查集的樹;
第一步:
遍歷過的元素{4}, 集合[4]{4}->4
第二步:
集合{4}與父節點{1}按秩合並, 合並後的集合為{4,1},集合代表元素為4,即father[4] = 4, father[1] = 4; 集合{4,1}的公共祖先為1,ancestor[4] = 1; 即這個集合的代表元素並不是它的公共祖先
第三步:
遍歷過的元素有{4,7}, 有兩個集合[4]{4,1}和[7]{7}, ([]裡面的元素為代表元素,{}的元素為集合內的所有元素), 此時, 若查詢(7,4), 則4已經遍歷過, 訪問4所在集合的代表元素為 father[4], 集合4的公共祖先為ancestor[father[4]]
第四步:
遍歷過的元素有{4,7,5}, 集合[7]{7}合並集合[5]{5}為[7]{7,5}, ancestor[7] = 5
.....
遍歷完根節點的第一棵子樹後, 集合[7]{4,1,5,7} 與根節點集合[0]{0}合並為[7]{0,1,4,5,7}, 即father[0]=7, 同時更新集合的公共祖先ancestor[7]=0;
最後遍歷過的元素{4,7,5,1,2,6,3,0}, 集合為[7]{4,7,5,1,2,6,3,0}, ancestor[7] = 0
為方便理解,最後的圖是沒有經過路徑壓縮的, 實際上應該是所有元素的父節點皆為集合代表元素7