樹狀結構之主席樹，樹狀主席樹

樹狀結構之主席樹，樹狀主席樹

主席樹搞了一個多星期TAT，，，，，，也只是大致領悟而已！！！

主席樹又稱函數式線段樹，顧名思義，也就是通過函數來實現的線段樹，至於為什麼叫主席樹，那是因為是fotile主席創建出來的這個數據結構（其實貌似是當初主席不會劃分樹而自己想出來的另一個處理方式。。。。是不是很吊呢？ ORZ...)不扯了，切入正題。

主席樹就是利用函數式編程的思想來使線段樹支持詢問歷史版本、同時充分利用它們之間的共同數據來減少時間和空間消耗的增強版的線段樹。

     很多問題如果用線段樹處理的話需要采用離線思想，若用主席樹則可直接在線處理。故很多時候離線線段樹求解可以轉化為在線主席樹求解。注意，主席樹本質就是線段樹，變化就在其實現可持久化，後一刻可以參考前一刻的狀態，二者共同部分很多。一顆線段樹的節點維護的是當前節點對應區間的信息，倘若每次區間都不一樣，就會給處理帶來一些困難。有時可以直接細分區間然後合並，此種情況線段樹可以直接搞定；但有時無法通過直接劃分區間來求解，如頻繁詢問區間第k小元素，當然，此問題有比較特殊的數據結構-劃分樹。其實還有一個叫做歸並樹，是根據歸並排序實現的，每個節點保存的是該區間歸並排序後的序列，因此，時間、空間復雜度都及其高， 所以一般不推薦去用。當然，主席樹也是可以解決的。

附上歸並樹代碼：

1 #include <cstdio> 2 #include <cstring> 3 #include <vector> 4 #include <algorithm> 5 using namespace std; 6 const int N = 100000 + 5; 7 8 vector<int>node[N << 2]; 9 10 int T, n, q, ql, qr, ans, k, sz; 11 12 int a[N], b[N]; 13 14 inline int read(){//快速讀入是邪教 15 char c; 16 int ret = 0; 17 int sgn = 1; 18 do{c = getchar();}while((c < '0' || c > '9') && c != '-'); 19 if(c == '-') sgn = -1; else ret = c - '0'; 20 while((c = getchar()) >= '0' && c <= '9') ret = ret * 10 + (c - '0'); 21 return sgn * ret; 22 } 23 24 void Build(int o, int l, int r){ 25 node[o].clear(); 26 if(l == r){ 27 node[o].push_back(a[l]); 28 return ; 29 } 30 int m = (l + r) >> 1; 31 Build(o << 1, l, m); 32 Build(o << 1|1, m + 1, r); 33 node[o].resize(r - l + 1); 34 merge(node[o<<1].begin(), node[o<<1].end(), node[o<<1|1].begin(), node[o<<1|1].end(), node[o].begin()); 35 } 36 37 int query(int o, int l, int r, int x){ 38 //if(ql > r || qr < l) return 0; 39 if(ql <= l && qr >= r) return upper_bound(node[o].begin(), node[o].end(), x) - node[o].begin(); 40 int m = (l + r) >> 1; 41 int ret = 0; 42 if(ql <= m)ret += query(o << 1, l, m, x); 43 if(qr > m)ret += query(o << 1|1, m + 1, r, x); 44 return ret; 45 } 46 47 void work(){ 48 //ql = read(); 49 //qr = read(); 50 //k = read(); 51 scanf("%d%d%d", &ql, &qr, &k); 52 int lt = 1, rt = sz; 53 while(lt <= rt){ 54 int md = (lt + rt) >> 1; 55 if(query(1, 1, n, b[md]) >= k)rt = md - 1; 56 else lt = md + 1; 57 } 58 printf("%d\n", b[rt+1]); 59 } 60 61 int main(){ 62 scanf("%d", &T); 63 while(T--){ 64 scanf("%d%d", &n, &q); 65 //n = read(); 66 //q = read(); 67 //for(int i = 1; i <= n; i ++) a[i] = b[i] = read(); 68 for(int i = 1; i <= n; i ++)scanf("%d", a + i), b[i] = a[i]; 69 Build(1, 1, n); 70 sort(b + 1, b + n + 1); 71 sz = unique(b + 1, b + n + 1) - (b + 1); 72 while(q --)work(); 73 } 74 return 0; 75 } View Code

 

赤果果的嫌棄，時間居然那麼費，，，，，，，（不過挺好理解的）

     主席樹的每個節點對應一顆線段樹，此處有點抽象。在我們的印象中，每個線段樹的節點維護的樹左右子樹下標以及當前節點對應區間的信息（信息視具體問題定）。對於一個待處理的序列a[1]、a[2]…a[n]，有n個前綴。每個前綴可以看做一棵線段樹，共有n棵線段樹；若不采用可持久化結構，帶來的嚴重後果就是會MLE，即對內存來說很難承受。根據可持久化數據結構的定義，由於相鄰線段樹即前綴的公共部分很多，可以充分利用，達到優化目的，同時每棵線段樹還是保留所有的葉節點只是較之前共用了很多共用節點。主席樹很重要的操作就是如何尋找公用的節點信息，這些可能可能出現在根節點也可能出現在葉節點。

下面是某大牛的理解：所謂主席樹呢，就是對原來的數列[1..n]的每一個前綴[1..i]（1≤i≤n）建立一棵線段樹，線段樹的每一個節點存某個前綴[1..i]中屬於區間[L..R]的數一共有多少個（比如根節點是[1..n]，一共i個數，sum[root] = i；根節點的左兒子是[1..(L+R)/2]，若不大於(L+R)/2的數有x個，那麼sum[root.left] = x）。若要查找[i..j]中第k大數時，設某結點x，那麼x.sum[j] - x.sum[i - 1]就是[i..j]中在結點x內的數字總數。而對每一個前綴都建一棵樹，會MLE，觀察到每個[1..i]和[1..i-1]只有一條路是不一樣的，那麼其他的結點只要用回前一棵樹的結點即可，時空復雜度為O(nlogn)。

我自己對主席樹的理解，是一個線段樹在修改一個值的時候，它只要修改logn個節點就可以了，那麼我們只要每次增加logn個節點就可以記錄它原來的狀態了, 即你在更新一個值的時候僅僅只是更新了一條鏈，其他的節點都相同，即達到共用。由於主席樹每棵節點保存的是一顆線段樹，維護的區間相同，結構相同，保存的信息不同，因此具有了加減性。（這是主席樹關鍵所在，當除筆者理解了很久很久，才相通的），所以在求區間的時候，若要處區間[l, r]， 只需要處理rt[r] - rt[l-1]就可以了，（rt[l-1]處理的是[1,l-1]的數，rt[r]處理的是[1,r]的數，相減即為[l, r]這個區間裡面的數。

比如說（以區間第k大為例hdu2665題目戳這裡http://acm.hdu.edu.cn/showproblem.php?pid=2665）:

設n = 4，q= 1;

4個數分別為4， 1， 3 ，2;

ql = 1, qr = 3, k = 2;

1.建樹

首先需要建立一棵空的線段樹，也是最原始的主席樹，此時主席樹只含一個空節點，此時設根節點為rt[0],表示剛開始的初值狀態，然後依次對原序列按某種順序更新，即將原序列加入到對應位置。此過程與線段樹一樣，時間復雜度為O（nlogn)，空間復雜度O（nlog(n))（筆者目前沒有完全搞清究竟是多少， 不過保守情況下，線段樹不會超過4*n）

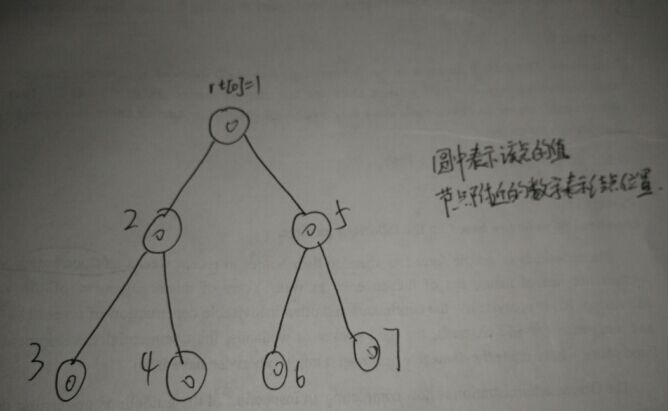
2.更新

 我們知道，更新一個葉節點只會影響根節點到該葉節點的一條路徑，故只需修改該路徑上的信息即可。每個主席樹的節點即每棵線段樹的結構完全相同，只是對應信息（可以理解為線段樹的結構完全一樣，只是對應葉子節點取值不同，從而有些節點的信息不同，本質是節點不同），此時可以利用歷史狀態，即利用相鄰的上一棵線段樹的信息。相鄰兩顆線段樹只有當前待處理的元素不同，其余位置完全一樣。因此，如果待處理的元素進入線段樹的左子樹的話，右子樹是完全一樣的，可以共用，即直接讓當前線段樹節點的右子樹指向相鄰的上一棵線段樹的右子樹；若進入右子樹，情況可以類比。此過程容易推出時間復雜度為O(logn)，空間復雜度為 O(logn)。如圖：

 3.查詢

先附上處理好之後的主席樹， 如圖:

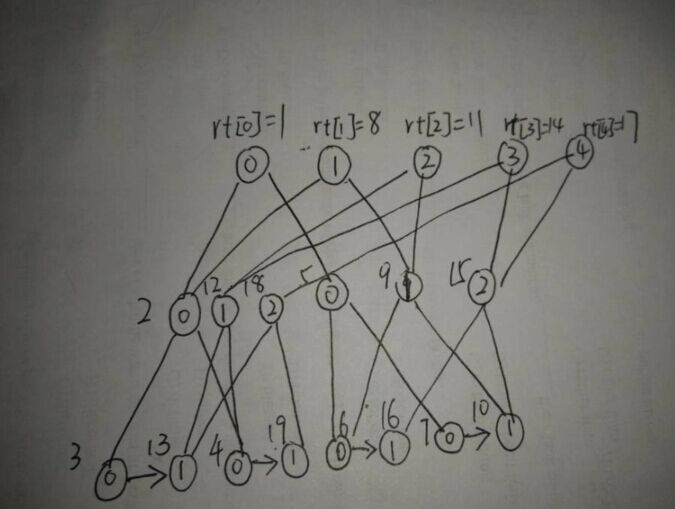
是不是看著很暈。。。。。。筆者其實也暈了，我們把共用的節點拆開來，看下圖：

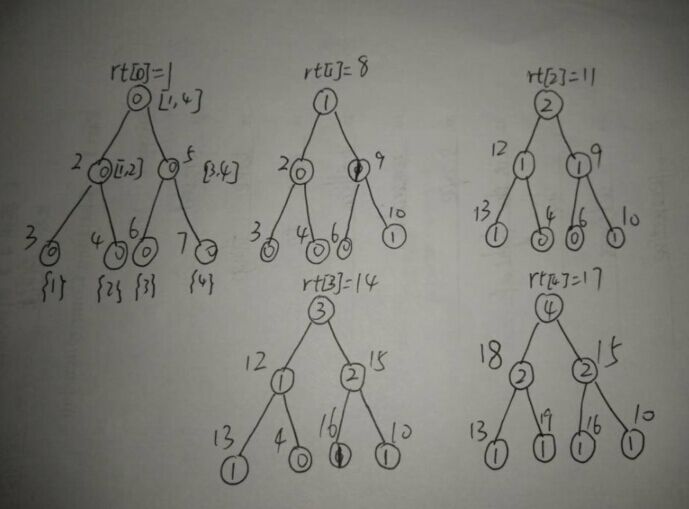
啊， 這下清爽多了，一眼看下去就知道每個節點維護的是哪棵線段樹了，TAT，如果早就這樣寫估計很快就明白了，rt[i]表示處理完前i個數之後所形成的線段樹，即具有了前綴和的性質，那麼rt[r] - rt[l-1]即表示處理的[l, r]區間喽。當要查詢區間[1,3]的時候，我們只要將rt[3] 和 rt[0]節點相減即可得到。如圖：

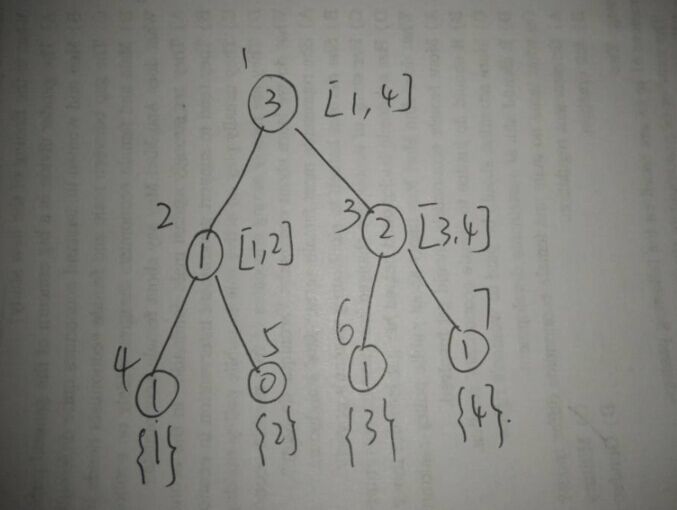
這樣我們得到區間[l, r]的數要查詢第k大便很容易了，設左節點中存的個數為cnt，當k<=cnt時，我們直接查詢左兒子中第k小的數即可，如果k>cnt，我們只要去查右兒子中第k-cnt小的數即可，這邊是一道很簡單的線段樹了。就如查找[1, 3]的第2小數（圖上為了方便，重新給節點標號），從根節點1向下搜，發現左兒子2的個數為1,1<2，所有去右兒子3中搜第2-1級第1小的數，然後再往下搜，發現左兒子6便可以了，此時已經搜到底端，所以直接返回節點6維護的值3即可就可以了。

附上代碼：

1 #include <cstdio> 2 #include <cstring> 3 #include <algorithm> 4 using namespace std; 5 const int N = 100000 + 5; 6 7 int a[N], b[N], rt[N * 20], ls[N * 20], rs[N * 20], sum[N * 20]; 8 9 int n, k, tot, sz, ql, qr, x, q, T; 10 11 void Build(int& o, int l, int r){ 12 o = ++ tot; 13 sum[o] = 0; 14 if(l == r) return; 15 int m = (l + r) >> 1; 16 Build(ls[o], l, m); 17 Build(rs[o], m + 1, r); 18 } 19 20 void update(int& o, int l, int r, int last, int p){ 21 o = ++ tot; 22 ls[o] = ls[last]; 23 rs[o] = rs[last]; 24 sum[o] = sum[last] + 1; 25 if(l == r) return; 26 int m = (l + r) >> 1; 27 if(p <= m) update(ls[o], l, m, ls[last], p); 28 else update(rs[o], m + 1, r, rs[last], p); 29 } 30 31 int query(int ss, int tt, int l, int r, int k){ 32 if(l == r) return l; 33 int m = (l + r) >> 1; 34 int cnt = sum[ls[tt]] - sum[ls[ss]]; 35 if(k <= cnt) return query(ls[ss], ls[tt], l, m, k); 36 else return query(rs[ss], rs[tt], m + 1, r, k - cnt); 37 } 38 39 void work(){ 40 scanf("%d%d%d", &ql, &qr, &x); 41 int ans = query(rt[ql - 1], rt[qr], 1, sz, x); 42 printf("%d\n", b[ans]); 43 } 44 45 int main(){ 46 scanf("%d", &T); 47 while(T--){ 48 scanf("%d%d", &n, &q); 49 for(int i = 1; i <= n; i ++) scanf("%d", a + i), b[i] = a[i]; 50 sort(b + 1, b + n + 1); 51 sz = unique(b + 1, b + n + 1) - (b + 1); 52 tot = 0; 53 Build(rt[0],1, sz); 54 //for(int i = 0; i <= 4 * n; i ++)printf("%d,rt = %d,ls = %d, rs = %d, sum = %d\n", i, rt[i], ls[i], rs[i], sum[i]); 55 for(int i = 1; i <= n; i ++)a[i] = lower_bound(b + 1, b + sz + 1, a[i]) - b; 56 for(int i = 1; i <= n; i ++)update(rt[i], 1, sz, rt[i - 1], a[i]); 57 for(int i = 0; i <= 5 * n; i ++)printf("%d,rt = %d,ls = %d, rs = %d, sum = %d\n", i, rt[i], ls[i], rs[i], sum[i]); 58 while(q --)work(); 59 } 60 return 0; 61 } View Code

看著這個時間的復雜度和歸並樹一比，從此對歸並樹無愛了，估計不會再用了。。。。ORZ~~

4.總結

由以上可知，主席樹是一種特殊的線段樹集，他幾乎具有所有線段樹的所有優勢，並且可以保存歷史狀態，以便以後加以利用，主席樹查找和更新時時間空間復雜度均為O（logn)， 且空間復雜度約為O(nlogn + nlogn)前者為空樹的空間復雜度，後者為更新n次的空間復雜度，主席樹的缺點就是空間耗損巨大，但還是可以接受的。當然主席樹不止這點應用，他可以處理許多區間問題，例如求區間[l, r]中的值介於[x,y]的值。總之應用多多。