HDU 4372 Count the Buildings(組合數學,第一類Stirling數)
HDU 4372
題意:有n個建築高度為1~n,從前看能看到f個,從後看能看到b個,求可能有多少種排序情況。
思路:
五個小時花了3.5小時在上面,結果靠強行yy出了遞推式(事後發現。。yy對了95%,跪在各種細節上,比賽結束也沒A掉。。
只能說大力出奇跡!但這種奇跡往往會毀在不經意的細節上orz
分析幾組數據我們可以發現,最高的n號樓一定是可以看到的,無論是從左還是右。
那麼民那桑,先固定住n號樓的位置,將n號樓左邊分為f-1組,右邊b-1組,且用每組最高的那個元素代表這一組;
而後我們可以發現樓n的左邊,從左到右,組與組之間最高的元素一定是單調遞增的!
且每組中的最高元素一定排在該組的最左邊,每組中的其它元素可以任意排列(相當於這個組中所有元素的環排列,所謂環排列就是一個元素位置固定其他元素自己動,方案數等於(n-1)!)。
右邊同理。
例如:n = 5 , b = 3 , f = 2。
顯然n號樓所在位置一定在第3,或第4:XX5XX或XXX5X
當位置在3之時,左邊2個元素分成2組,顯然符合結論;
當位置在4之時,左邊3個元素分成2組,左邊可能的情況為:1 32 5X,21 3 5X ,2 31 5X , 1 42 5X ,21 4 5X ,2 41 5X ,1 43 5X ,31 4 5X ,3 41 5X...
均滿足結論(當然這裡的X很明顯已經求出來了XP
故我們可以先把n-1個元素分成f-1+b-1組,每組做環排列,累計方案數即是答案。
而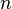 個人分成
個人分成 組做環排列的方法數目,我們稱之為第一類stirling數
組做環排列的方法數目,我們稱之為第一類stirling數
答案:ans(n, f, b) = C[f + b - 2][f - 1] * S[n - 1][f + b - 2];
code:
/*
* @author Novicer
* language : C++/C
*/
#include
#include
#include
#include
#include
#include
#include
#include
#include
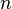 個人分成
個人分成 組做環排列的方法數目,我們稱之為第一類stirling數
組做環排列的方法數目,我們稱之為第一類stirling數