1. 概述
位圖(bitmap)是一種非常常用的結構,在索引,數據壓縮等方面有廣泛應用。本文介紹了位圖的實現方法及其應用場景。
2. 位圖實現

(1)自己實現
在位圖中,每個元素為“0”或“1”,表示其對應的元素不存在或者存在。
#define INT_BITS sizeof(int)
#define SHIFT 5 // 2^5=32
#define MASK 0x1f // 2^5=32
#define MAX 1024*1024*1024 //max number
int bitmap[MAX / INT_BITS];
/*
* 設置第i位
* i >> SHIFT 相當於 i / (2 ^ SHIFT),
* i&MASK相當於mod操作 m mod n 運算
*/
void set(int i) {
bitmap[i >> SHIFT] |= 1 << (i & MASK);
}
//獲取第i位
int test(int i) {
return bitmap[i >> SHIFT] & (1 << (i & MASK));
}
//清除第i位
int clear(int i) {
return bitmap[i >> SHIFT] & ~(1 << (i & MASK));
}
(2)函數庫實現
C++的STL中有bitmap類,它提供了很多方法,詳見:http://www.cplusplus.com/reference/stl/bitset/
3. 位圖應用
3.1 枚舉
(1)全組合
字符串全組合枚舉(對於長度為n的字符串,組合方式有2^n種),如:abcdef,可以構造一個從字符串到二進制的映射關系,通過枚舉二進制來進行全排序。
null——> 000000 f——> 000001 e——> 000010 ef——> 000011 …… abcedf——> 111111
(2)哈米爾頓距離

枚舉算法,復雜度是O(N^2),怎樣降低復雜度呢?
如果是N 個二維的點,那麼我們可以怎麼用較快的方法求出

通過簡單的數學變形,我們可以得到這樣的數學公式:
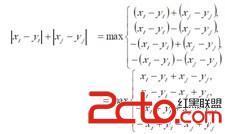
通過觀察,我們發現每一對相同元的符號必定相反,如:x_i-y_i,於是我們有了一個二進制思想的思路,那就是枚舉這些二i維的點的x 軸y 軸前的正負號,這樣就可以用一個0~3 的數的二進制形式來表示每個元素前面的正負號,1表示+號,0表示−號,如:2 表示的二進制位形式為10表示x_i-y_i。這樣我們就可以通過2^2*N次記錄下這些二元組的不同的符號的數值,對於每個二進制來表示的不同的式子只需記錄下他們的值,這樣我們只需求max_i 和min_i出這些相同的二進制表示的式子max_i –min_i,最後我們就可以解出ans=max{max_i-min_i}。
通過位圖,算法時間復雜度可將為O(N)。
3.2 搜索
設計搜索剪枝時,需要保存已經搜索過的歷史信息,有些情況下,可以使用位圖減小歷史信息數據所占空間。
3.3 壓縮
(1)在2.5億個整數中找出不重復的整數,注,內存不足以容納這2.5億個整數?
(2)騰訊面試題:給40億個不重復的unsigned int的整數,沒排過序的,然後再給一個數,如何快速判斷這個數是否在那40億個數當中?
4. 總結
Bitmap是一種非常簡潔快速的數據結構,他能同使證存儲空間和速度最優化(而不必空間換時間)。