Partition（hdu4651）2013 Multi-University Training Contest 5，partition

Partition（hdu4651）2013 Multi-University Training Contest 5，partition

Partition

Time Limit: 6000/3000 MS (Java/Others) Memory Limit: 32768/32768 K (Java/Others) Total Submission(s): 954 Accepted Submission(s): 545

Problem Description How many ways can the numbers 1 to 15 be added together to make 15? The technical term for what you are asking is the "number of partition" which is often called P(n). A partition of n is a collection of positive integers (not necessarily distinct) whose sum equals n.

Now, I will give you a number n, and please tell me P(n) mod 1000000007.  

Input The first line contains a number T(1 ≤ T ≤ 100), which is the number of the case number. The next T lines, each line contains a number n(1 ≤ n ≤ 10⁵) you need to consider.

 

Output For each n, output P(n) in a single line.  

Sample Input 4 5 11 15 19  

Sample Output 7 56 176 490  

Source 2013 Multi-University Training Contest 5      題意：問一個數n能被拆分成多少種方法   首先你要知道母函數+然後你要知道五邊形數定理；  

設第n個五邊形數為，那麼，即序列為：1, 5, 12, 22, 35, 51, 70, ...

 

對應圖形如下：

 

 

設五邊形數的生成函數為，那麼有：

 

 

 

 

以上是五邊形數的情況。下面是關於五邊形數定理的內容：

 

五邊形數定理是一個由歐拉發現的數學定理，描述歐拉函數展開式的特性。歐拉函數的展開式如下：

 

 

 

歐拉函數展開後，有些次方項被消去，只留下次方項為1, 2, 5, 7, 12, ...的項次，留下來的次方恰為廣義五邊形數。

 

 

五邊形數和分割函數的關系

 

歐拉函數的倒數是分割函數的母函數，亦即：

 

   其中為k的分割函數。

 

上式配合五邊形數定理，有：

 

 

  在 n>0 時，等式右側的系數均為0，比較等式二側的系數，可得  

 

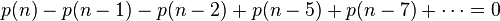
因此可得到分割函數p(n)的遞歸式：

 

例如n=10時，有：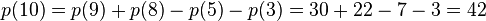

 

 

所以，通過上面遞歸式，我們可以很快速地計算n的整數劃分方案數p(n)了。

 

詳見維基百科：https://zh.wikipedia.org/wiki/%E4%BA%94%E8%A7%92%E6%95%B0#.E5.BB.A3.E7.BE.A9.E4.BA.94.E9.82.8A.E5.BD.A2.E6.95.B8 或 https://zh.wikipedia.org/wiki/%E4%BA%94%E9%82%8A%E5%BD%A2%E6%95%B8%E5%AE%9A%E7%90%86    轉載請注明出處：http://blog.csdn.net/u010579068    題目鏈接：http://acm.hdu.edu.cn/showproblem.php?pid=4651

 

#include<iostream>
#include<cstdio>
#define NN 100005
#define LL __int64
#define mod 1000000007

using namespace std;
LL wu[NN],pa[NN];
void init()
{
    pa[0]=1;
    pa[1]=1;
    pa[2]=2;
    pa[3]=3;
    LL ca=0;
    for(LL i=1;i<=100000/2;i++)
    {
        wu[ca++]=i*(3*i-1)/2;
        wu[ca++]=i*(3*i+1)/2;
        if(wu[ca-1]>100000) break;
    }
    for(LL i=4;i<=100000;i++)
    {
        pa[i]=(pa[i-1]+pa[i-2])%mod;
        ca=1;
        while(wu[2*ca]<=i)
        {
            if(ca&1)
            {
                pa[i]=(pa[i]-pa[i-wu[2*ca]])%mod;
                pa[i]=(pa[i]%mod+mod)%mod;
                if(wu[2*ca+1]<=i)
                    pa[i]=(pa[i]-pa[i-wu[2*ca+1]])%mod;
                pa[i]=(pa[i]%mod+mod)%mod;
            }
            else
            {
                pa[i]=(pa[i]+pa[i-wu[2*ca]])%mod;
                pa[i]=(pa[i]%mod+mod)%mod;
                if(wu[2*ca+1]<=i)
                    pa[i]=(pa[i]+pa[i-wu[2*ca+1]])%mod;
                pa[i]=(pa[i]%mod+mod)%mod;
            }
            ca++;
        }
    }
}
int main()
{
    int T,n;
    init();
    scanf("%d",&T);
    while(T--)
    {
        scanf("%d",&n);
        printf("%I64d\n",pa[n]);
    }
    return 0;

}