Codeforces Round #310 (Div. 1) D. Case of a Top Secret 二分 stl應用

Codeforces Round #310 (Div. 1) D. Case of a Top Secret 二分 stl應用

D. Case of a Top Secret
time limit per test2 seconds
memory limit per test256 megabytes
inputstandard input
outputstandard output
Andrewid the Android is a galaxy-famous detective. Now he is busy with a top secret case, the details of which are not subject to disclosure.

However, he needs help conducting one of the investigative experiment. There are n pegs put on a plane, they are numbered from 1 to n, the coordinates of the i-th of them are (xi, 0). Then, we tie to the bottom of one of the pegs a weight on a tight rope of length l (thus, its coordinates will be equal to (xi,  - l), where i is the number of the used peg). Then the weight is pushed to the right, so that it starts to rotate counterclockwise. At the same time, if the weight during rotation touches some of the other pegs, it then begins to rotate around that peg. Suppose that each peg itself is very thin and does not affect the rope length while weight is rotating around it.

More formally, if at some moment the segment of the rope contains one or more pegs in addition to the peg around which the weight is rotating, the weight will then rotate around the farthermost one of them on a shorter segment of a rope. In particular, if the segment of the rope touches some peg by its endpoint, it is considered that the weight starts to rotate around that peg on a segment of the rope of length 0.

At some moment the weight will begin to rotate around some peg, without affecting the rest of the pegs. Andrewid interested in determining the number of this peg.

Andrewid prepared m queries containing initial conditions for pushing the weight, help him to determine for each of them, around what peg the weight will eventually rotate.

Input
The first line contains integers n and m (1 ≤ n, m ≤ 2·105) — the number of pegs and queries.

The next line contains n integers x1, x2, …, xn ( - 109 ≤ xi ≤ 109) — the coordinates of the pegs. It is guaranteed that the coordinates of all the pegs are distinct integers.

Next m lines contain the descriptions of the queries of pushing the weight, each consists of two integers ai (1 ≤ ai ≤ n) and li (1 ≤ li ≤ 109) — the number of the starting peg and the length of the rope.

Output
Print m lines, the i-th line should contain the number of the peg around which the weight will eventually rotate after the i-th push.

Sample test(s)
input
3 2
0 3 5
2 3
1 8
output
3
2
input
4 4
1 5 7 15
1 4
2 15
3 16
1 28
output
2
4
3
1
Note
Picture to the first sample test:

Picture to the second sample test:

Note that in the last query weight starts to rotate around the peg 1 attached to a rope segment of length 0.
題意是，數軸上有相異的n個點，選一個起點和一個起始長度的繩子繞著這些個釘子轉，輸出最終圍著哪個釘子轉！
向下轉的時候，就是要找小於等於最遠距離的點，向上轉大於等於最遠距離的點，所以圖簡單就直接用set做了，當然也可以自已寫二分。這不是關鍵，這題，主要是有一個重大的優化如圖

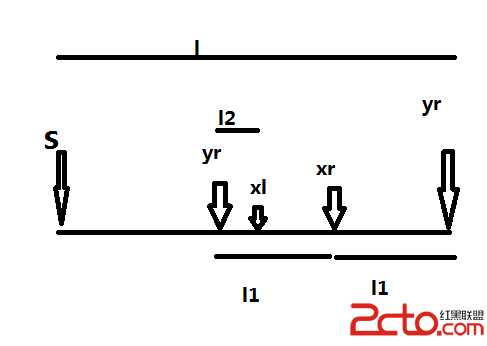
上圖中的公式就是代碼中的公式也容易就不說了，看下面這圖

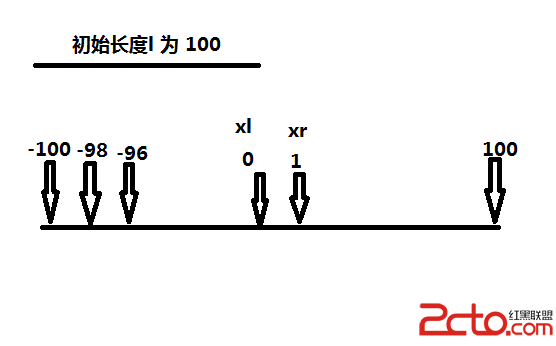
明顯，一直在繞著xl xr轉圈，所以直接用 l % (l - l2),就可以大大加速處理的速度。總體復雜度k * n * logn了！

#define INF         9000000000
#define EPS         (double)1e-9
#define mod         1000000007
#define PI          3.14159265358979
//*******************************************************************************/
#endif
#define N 200050
#define M 100005
#define maxn 205
#define MOD 1000000000000000007
int n,x[N],m,l,s,xl,xr,lxl,lxr,l1,l2,yl,yr,inx;
set myset;
set::iterator it;

//適用於正負整數
template 
inline bool scan_d(T &ret) {
   char c; int sgn;
   if(c = getchar(),c == EOF) return 0; //EOF
   while(c != '-' && (c < '0' || c > '9')) c = getchar();
   sgn = (c == '-') ? -1 : 1;
   ret = (c == '-') ? 0 : (c - '0');
   while(c = getchar(),c >= '0' && c <= '9') ret = ret * 10 + (c - '0');
   ret *= sgn;
   return 1;
}

inline void out(int x) {
   if(x > 9) out(x / 10);
   putchar(x % 10 + '0');
}
int main()
{
    while(S2(n,m)!=EOF)
    {
        myset.clear();
        for(int i=1;i<=n;i++) {
            scan_d(x[i]);
            myset.insert(make_pair(x[i],i));
        }
        FI(m){
            scan_d(inx);scan_d(l);
            lxr = lxl = -1; s = x[inx];
            while(true){
                yr = s + l;
                it = myset.upper_bound(make_pair(yr,N + 1));
                it --;
                xr = x[it->second];
                l1 = yr - xr;
                yl = xr - (yr - xr);
                it = myset.lower_bound(make_pair(yl,-1));
                xl = x[it->second];
                l2 = xl - yl;
                if(l2 == l){
                    out(it->second);
                    putchar('
');
                    break;
                }
                else {
                    if(lxl == xl && lxr == xr){
                        l = l % (l - l2);
                    }
                    else {
                        l = l2;
                    }
                    s = xl;
                    lxl = xl;lxr = xr;
                }
            }
        }
    }
    return 0;
}