大家好,我是小Hi和小Ho的小伙伴Nettle,從這個星期開始由我來完成我們的Weekly。
新年回家,又到了一年一度大齡剩男剩女的相親時間。Nettle去姑姑家玩的時候看到了一張姑姑寫的相親情況表,上面都是姑姑介紹相親的剩男剩女們。每行有2個名字,表示這兩個人有一場相親。由於姑姑年齡比較大了記性不是太好,加上相親的人很多,所以姑姑一時也想不起來其中有些人的性別。因此她拜托我檢查一下相親表裡面有沒有錯誤的記錄,即是否把兩個同性安排了相親。
OK,讓我們愉快的暴力搜索吧!
才怪咧。
對於拿到的相親情況表,我們不妨將其轉化成一個圖。將每一個人作為一個點(編號1..N),若兩個人之間有一場相親,則在對應的點之間連接一條無向邊。(如下圖)
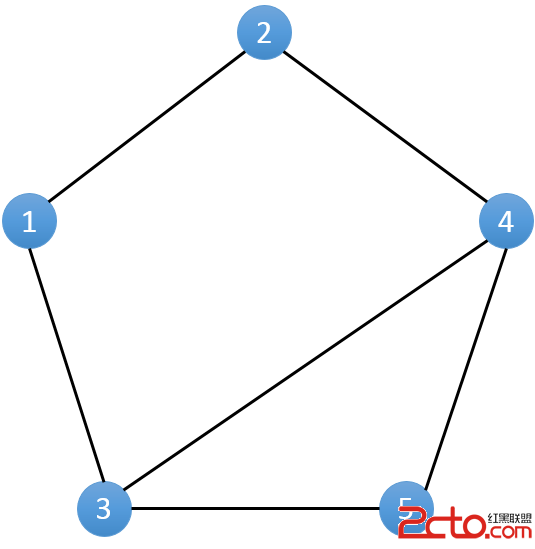
因為相親總是在男女之間進行的,所以每一條邊的兩邊對應的人總是不同性別。假設表示男性的節點染成白色,女性的節點染色黑色。對於得到的無向圖來說,即每一條邊的兩端一定是一白一黑。如果存在一條邊兩端同為白色或者黑色,則表示這一條邊所表示的記錄有誤。
由於我們並不知道每個人的性別,我們的問題就轉化為判定是否存在一個合理的染色方案,使得我們所建立的無向圖滿足每一條邊兩端的頂點顏色都不相同。
那麼,我們不妨將所有的點初始為未染色的狀態。隨機選擇一個點,將其染成白色。再以它為起點,將所有相鄰的點染成黑色。再以這些黑色的點為起點,將所有與其相鄰未染色的點染成白色。不斷重復直到整個圖都染色完成。(如下圖)
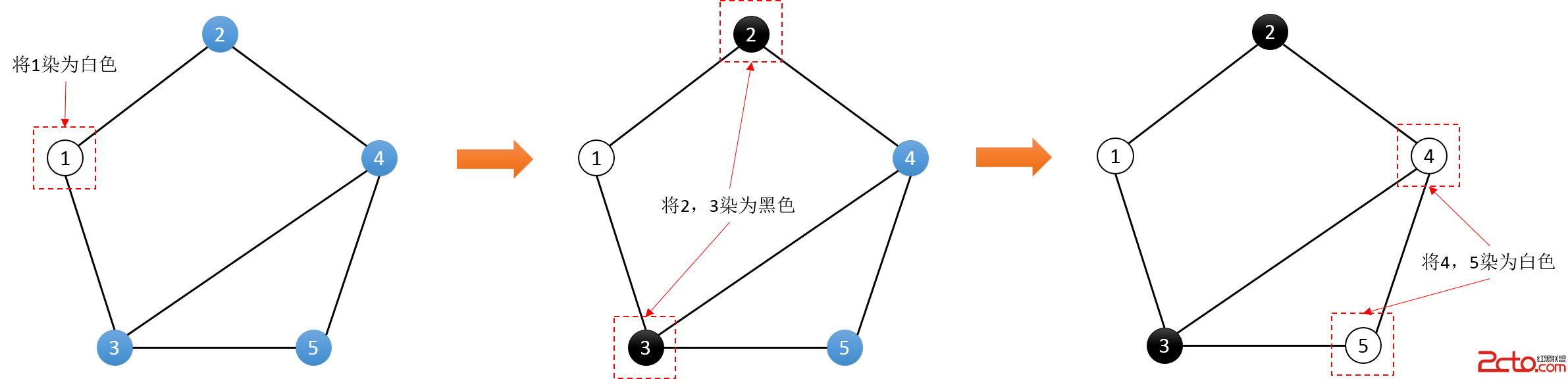
在染色的過程中,我們應該怎樣發現錯誤的記錄呢?相信你一定發現了吧。對於一個已經染色的點,如果存在一個與它相鄰的已染色點和它的顏色相同,那麼就一定存在一條錯誤的記錄。(如上圖的4,5節點)
到此我們就得到了整個圖的算法:
接下來就動手寫寫吧!
第1行:1個正整數T(1≤T≤10)
接下來T組數據,每組數據按照以下格式給出:
第1行:2個正整數N,M(1≤N≤10,000,1≤M≤40,000)
第2..M+1行:每行兩個整數u,v表示u和v之間有一條邊
第1..T行:第i行表示第i組數據是否有誤。如果是正確的數據輸出”Correct”,否則輸出”Wrong”
2 5 5 1 2 1 3 3 4 5 2 1 5 5 5 1 2 1 3 3 4 5 2 3 5
Wrong Correct
好久沒寫代碼,,繼續攢點模板!
AC代碼:
#include#include #include #include #include #include using namespace std; int T; int n, m; const int maxn = 10005; vector G[maxn]; bool vis[maxn]; int f[maxn]; int bfs(int i) { queue que; que.push(i); vis[i] = true; f[i] = 0; while(!que.empty()) { int e = que.front(); que.pop(); int d = G[e].size(); // cout << e << endl; for(int i = 0; i < d; i ++) { int t = G[e][i]; // cout << t << ; if(vis[t]) { if(f[t] == f[e]) return 1; } else { vis[t] = true; f[t] = f[e] == 0 ? 1 : 0; que.push(t); } } // cout << endl; } return 0; } int fun() { //注意可能會有多個連通分量 for(int i = 1; i <= n; i ++) { if(!vis[i]) { if(bfs(i) == 1) return 1; } } return 0; } int main() { scanf(%d, &T); while(T --) { // for(int i = 0; i < maxn; i ++) G[i].clear(); scanf(%d %d, &n, &m); for(int i = 0; i < m; i ++) { int u, v; scanf(%d %d, &u, &v); G[u].push_back(v); G[v].push_back(u); } memset(vis, false, sizeof(vis)); if(fun() == 1) { printf(Wrong ); } else printf(Correct ); // for(int i = 1; i <= n; i ++) { // cout << f[i] << ; // } for(int i = 1; i <= n; i ++) G[i].clear(); } return 0; }