leetcode | Implement strStr() | 實現字符串查找函數

leetcode | Implement strStr() | 實現字符串查找函數

Returns the index of the first occurrence of needle in haystack, or -1 if needle is not part of haystack.
如：haystack = “bcbcda”; needle = “bcd” 則 return 2

解析：字符串查找函數，strstr()函數用來檢索子串在字符串中首次出現的位置，其原型為：
char *strstr( char *str, char * substr );

思路一：容易實現，然並卵（時間復雜度不滿足要求）

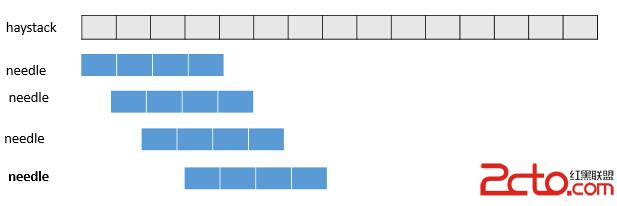
兩個指針，i 指向haystack 的起始，j 指向 needle 的起始；首先 i 向後走，直至haystack[i] == needle [j]; 然後 j 往後走，如果haystack[i+j] != needle [j] 跳出，如果能走 m 步，即存在相同,返回i；如果存在不匹配，則haystack 後移後，從needle[0]重新比較
原理就是：拿著 needle 字符串 去 haystack 上逐個比較；每次最多需要對比m次，最多重復n次；
故時間復雜度為O(m*n),不能滿足leetcode的時間要求
注：在寫代碼前理清思路，
1. 確定解決問題的算法
2. 確定算法的時空復雜度，考慮能不能優化或詢問面試官是否要求時空復雜度。
3. 有哪些特殊情況需要處理
必須必須必須先清晰思路，再寫代碼。

int strStr2(string haystack, string needle) {
        // 時間復雜度O(m*n),不能滿足leetcode的時間要求
        int m = needle.size();
        int n = haystack.size();
        if (m == 0) return 0;
        if (m > n) return -1;
        for (int i = 0; i < n; i++) {
            int j = 0;
            if (haystack[i] == needle[j]) {
                for (; j < m && i+j < n; j++) {
                    if (needle[j] != haystack[i+j])
                        break;
                }
                if (j == m)
                    return i;
            }
        }
        return -1;
    }

思路二 Rabin–Karp algorithm算法 - Hash 查找

Rabin–Karp algorithm算法：是計算機科學中通過 hash 的方法用於在一個大量文本中查找一個固定長度的字符串的算法。（模式查找）

從思路一我們可知，要想確定haystack中存在needle，必須完全比較needle的所有字符。那麼有沒有能夠利用上一次比較的結果，僅添加O(1)的時間。
基本思想是：用一個hash code 表示一個字符串，為了保證 hash 的唯一性，我們用比字符集大的素數為底，以這個素數的冪為基。
例如：小寫字母集，選擇素數29為底，如字符串”abcd”的hash code為
hash=1∗290+2∗291+3∗292+4∗293，
那麼下一步計算字符串”bcde”的 hash code 為hash=hash/29+5∗293 這一計算過程是O(1) 常量的操作，那麼檢測所有子串所需的時間復雜度是O(m+(n-m)) = O(n)是一個線性算法（Rolling hash）
<注>例子中是正序計算的hash code，以下程序中使用是倒序計算的 hash code, 即
hash(abcd)=4∗290+3∗291+2∗292+1∗293,類似於進制轉換
hash(bcde)=(hash(abcd)−1∗293)∗29+5

    int charToInt(char c) {
        return (int)(c-'a'+1);
    }
    // 時間復雜度 O(m+(n-m)) = O(n)
    int strStr(string haystack, string needle) {
        int m = needle.size();
        int n = haystack.size();
        if (m == 0) return 0;
        if (m > n) return -1;

        const int base = 29;
        long long max_base = 1;
        long long needle_code = 0;
        long long haystack_code = 0;
        for (int j = m - 1; j >= 0; j--) {
            needle_code += charToInt(needle[j])*max_base;
            haystack_code += charToInt(haystack[j])*max_base;
            max_base *= base;
        }
        max_base /= base; // 子串的最大基
        if (haystack_code == needle_code)
            return 0;
        for (int i = m; i < n; i++) {
            haystack_code = (haystack_code - charToInt(haystack[i-m]) * max_base) * base + charToInt(haystack[i]);
            if (haystack_code == needle_code)
                return i - m + 1;
        }
        return -1;
    }

存在的缺點是，素數的冪可能會很大，因此計算結果要使用 long long 的類型 ，甚至要求更大的big int；另外，可以通過取余的方式縮小，但是有小概率誤判。