第一種:
主要是利用 樹結點類型的數組、二叉樹結點序號之間的關系 來創建:
父結點序號為 i 則,左兒子結點序號為 2*i ,右兒子序號為 2*i+1.
//用層次遍歷的方法來創建二叉樹
#include <iostream>
#include <queue>
using namespace std;
//二叉鏈表的結構類型定義
const int maxsize=1024;
typedef char datatype;
typedef struct node
{
datatype data;
struct node *lchild,*rchild;
}bitree;
bitree*creattree();
void PreOrder(bitree*);
//TestCase: ebfad.g..c#
void main()
{
bitree* pb = creattree();
PreOrder(pb);
cout<<endl;
system("pause");
}
//層次遍歷建立二叉樹 1
bitree* creattree()
{
char ch;
int front = 1,rear = 0;
bitree *root, *s;
root = NULL;
bitree *Q[maxsize];
//front是用來指向父結點下標的。
printf("按層次輸入二叉樹,虛結點輸入'.',以'#'結束輸入:\n");
while( (ch=getchar()) != '#' )
{
s = NULL;
if(ch!='.')
{
//為結點分配空間和設置數據域,指針域
s=(bitree*)malloc(sizeof(bitree));
s->data = ch;
s->lchild = NULL; s->rchild = NULL;
}
//輸入一個結點就放到數組裡
rear ++;
Q[rear] = s;
//根結點:
if(rear == 1)
root = s;
else
{
//如果是虛結點,則申請不到s就不必考慮怎麼掛結點s
if( s && Q[front])
{
//下標為偶數的話就掛在左子樹上
if( rear%2== 0)
Q[front]-> lchild = s;
//下標為奇數就掛在右邊
else
Q[front]-> rchild = s;
}
//放好兩個結點之後就要改變父結點的下標了
if(rear%2 == 1)
front++;
}
}
return root;
}
//先序遍歷輸出
void Visit(bitree* T)
{
if(T->data != '#')
{
printf("%c ",T->data);
}
}
void PreOrder(bitree* T){
if(T != NULL){
Visit(T);
PreOrder(T->lchild);
PreOrder(T->rchild);
}
}
第二種:
用隊列來輔助完成二叉樹的層次創建。
(1)第一步很特殊,首先是樹根
Binary_node* pNode=A.front();
A.pop();
B.push(pNode);
A:bfad.g..c
B:e
樹:

(2)後面的每一步都是從A中取出兩個隊首,放入B隊列尾部(如果為NULL則不放)。從B中取出隊首,隊列A中取出的元素正好是B中取出元素的小孩子
Binary_node* pfather= B.front();
B.pop();
Binary_node* pLchild= A.front();//先出來的是左孩子
A.pop();
Binary_node* pRchild= A.front();
A.pop();
pfather->left=pLchild;
pfather->right=pRchild;
//先放入左孩子
if(pLchild!=NULL)
{
B.push(pLchild);
}
if(pRchild!=NULL)
{
B.push(pRchild);
}
A:ad.g..c
B:bf
樹:

(3)
A:.g..c
B:fad
樹:
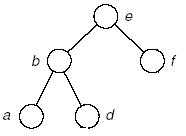
(4)
A:..c
B:adg
樹:
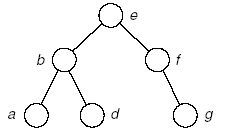
(5)
A:c
B:dg
樹:
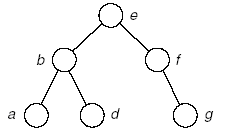
(6)
A:空(當隊列A為空的時候整個算法結束,樹構造成功)
B:g
樹:
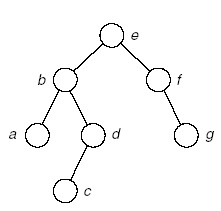
完成。
buildTree(Binary_node * &root)
{
char nodeData;//結點中的數據
queue<char> treeDataQueue;
queue< Binary_node * > treeNodeQueue;//
queue<Binary_node * > treeFatherQueue;//
Binary_node *pTreeNode;//從樹結點隊列中彈出的結點
Binary_node *pfather ;
Binary_node *pLchild;
Binary_node *pRchild;
while(!treeDataQueue.empty()){
nodeData = treeDataQueue.front();
treeDataQueue.pop();
if(nodeData!='.')
pTreeNode = new Binary_node(nodeData);
else pTreeNode = NULL;
treeNodeQueue.push(pTreeNode);
}
//根結點
pTreeNode = treeNodeQueue.front();
treeNodeQueue.pop();
root = pTreeNode;
treeFatherQueue.push(pTreeNode);
while(!treeNodeQueue.empty()){
pfather = treeFatherQueue.front();
treeFatherQueue.pop();
pLchild = treeNodeQueue.front();
treeNodeQueue.pop();
if(pLchild!=NULL){
pfather->left = pLchild;
treeFatherQueue.push(pLchild);
}
if(!treeNodeQueue.empty()){
pRchild = treeNodeQueue.front();
treeNodeQueue.pop();
if(pRchild!=NULL){
pfather->right = pRchild;
treeFatherQueue.push(pRchild);
}//end if(pRchild!=NULL)
}//end if(!treeNodeQueue.empty())
}//end while(!treeNodeQueue.empty())
}