程式師世界 >> 編程語言 >> C語言 >> C++ >> C++入門知識 >> Codeforces Round #304 (Div. 2)，

Codeforces Round #304 (Div. 2)，

編輯：C++入門知識

Codeforces Round #304 (Div. 2)，

A. Soldier and Bananas

A soldier wants to buy w bananas in the shop. He has to pay k dollars for the first banana, 2k dollars for the second one and so on (in other words, he has to pay i·k dollars for the i-th banana).

He has n dollars. How many dollars does he have to borrow from his friend soldier to buy w bananas?

Input

The first line contains three positive integers k, n, w (1 ≤ k, w ≤ 1000, 0 ≤ n ≤ 109), the cost of the first banana, initial number of dollars the soldier has and number of bananas he wants.

Output

Output one integer — the amount of dollars that the soldier must borrow from his friend. If he doesn't have to borrow money, output 0.

Sample test(s) input

3 17 4

output

 1 #include <stdio.h>
 2 #include <string.h>
 3 #include <algorithm>
 4 using namespace std;
 5 
 6 #define LL __int64
 7 LL n,k,w;
 8 
 9 int main()
10 {
11     int i;
12     LL sum = 0;
13     scanf("%I64d%I64d%I64d",&k,&n,&w);
14     for(i = 1;i<=w;i++)
15         sum +=i*k;
16         if(n>=sum)
17             printf("0\n");
18         else
19     printf("%I64d\n",sum-n);
20 
21     return 0;
22 }

B. Soldier and Badges

Colonel has n badges. He wants to give one badge to every of his n soldiers. Each badge has a coolness factor, which shows how much it's owner reached. Coolness factor can be increased by one for the cost of one coin.

For every pair of soldiers one of them should get a badge with strictly higher factor than the second one. Exact values of their factors aren't important, they just need to have distinct factors.

Colonel knows, which soldier is supposed to get which badge initially, but there is a problem. Some of badges may have the same factor of coolness. Help him and calculate how much money has to be paid for making all badges have different factors of coolness.

Input

First line of input consists of one integer n (1 ≤ n ≤ 3000).

Next line consists of n integers ai (1 ≤ ai ≤ n), which stand for coolness factor of each badge.

Output

Output single integer — minimum amount of coins the colonel has to pay.

Sample test(s) input

4
1 3 1 4

output

input

5
1 2 3 2 5

output

Note

In first sample test we can increase factor of first badge by 1.

In second sample test we can increase factors of the second and the third badge by 1.

題意：給你n堆價值，要求得到每堆價值是獨一無二的，問你往每堆加多少，最少加多少。

思路：（貪心）先排序，然後以第一個為基准，後面的不大於前面的，就加加；

轉載請注明出處：尋找&星空の孩子

題目鏈接：http://codeforces.com/contest/546/problem/B

 1 #include <iostream>
 2 #include <stdio.h>
 3 #include <string.h>
 4 #include <string>
 5 #include <stack>
 6 #include <queue>
 7 #include <map>
 8 #include <set>
 9 #include <vector>
10 #include <math.h>
11 #include <bitset>
12 #include <list>
13 #include <algorithm>
14 #include <climits>
15 using namespace std;
16 
17 #define lson 2*i
18 #define rson 2*i+1
19 #define LS l,mid,lson
20 #define RS mid+1,r,rson
21 #define UP(i,x,y) for(i=x;i<=y;i++)
22 #define DOWN(i,x,y) for(i=x;i>=y;i--)
23 #define MEM(a,x) memset(a,x,sizeof(a))
24 #define W(a) while(a)
25 #define gcd(a,b) __gcd(a,b)
26 #define LL long long
27 #define N 5000005
28 #define INF 0x3f3f3f3f
29 #define EXP 1e-8
30 #define lowbit(x) (x&-x)
31 const int mod = 1e9+7;
32 #define LL __int64
33 int n,a[3005];
34 int main()
35 {
36     int i,j,ans;
37     while(~scanf("%d",&n))
38     {
39         ans = 0;
40         int sum1 = 0,sum2 = 0;
41         for(i = 1; i<=n; i++)
42         {
43             scanf("%d",&a[i]);
44             sum1+=a[i];
45         }
46         sort(a+1,a+1+n);
47         sum2 = a[1];
48         for(i = 2; i<=n; i++)
49         {
50             if(a[i] == a[i-1])
51                 a[i]++;
52             else if(a[i]<a[i-1])
53                 a[i] +=(a[i-1]-a[i])+1;
54             sum2+=a[i];
55         }
56         printf("%d\n",sum2-sum1);
57     }
58 
59     return 0;
60 }

C. Soldier and Cards

Two bored soldiers are playing card war. Their card deck consists of exactly n cards, numbered from 1 to n, all values are different. They divide cards between them in some manner, it's possible that they have different number of cards. Then they play a "war"-like card game.

The rules are following. On each turn a fight happens. Each of them picks card from the top of his stack and puts on the table. The one whose card value is bigger wins this fight and takes both cards from the table to the bottom of his stack. More precisely, he first takes his opponent's card and puts to the bottom of his stack, and then he puts his card to the bottom of his stack. If after some turn one of the player's stack becomes empty, he loses and the other one wins.

You have to calculate how many fights will happen and who will win the game, or state that game won't end.

Input

First line contains a single integer n (2 ≤ n ≤ 10), the number of cards.

Second line contains integer k1 (1 ≤ k1 ≤ n - 1), the number of the first soldier's cards. Then follow k1 integers that are the values on the first soldier's cards, from top to bottom of his stack.

Third line contains integer k2 (k1 + k2 = n), the number of the second soldier's cards. Then follow k2 integers that are the values on the second soldier's cards, from top to bottom of his stack.

All card values are different.

Output

If somebody wins in this game, print 2 integers where the first one stands for the number of fights before end of game and the second one is 1 or 2 showing which player has won.

If the game won't end and will continue forever output - 1.

Sample test(s) input

4
2 1 3
2 4 2

output

6 2

input

3
1 2
2 1 3

output

-1

Note

First sample:

$\text{[math]}$

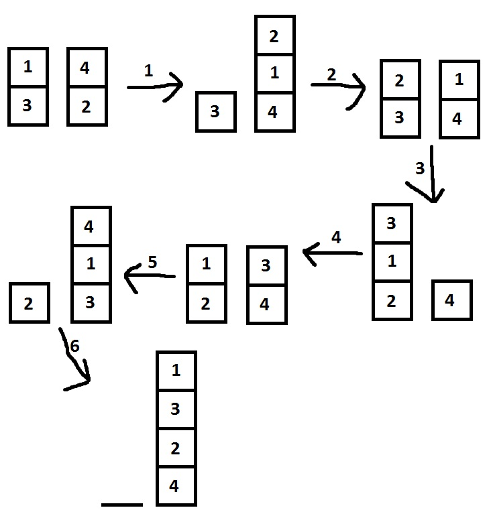
Second sample:

$\text{[math]}$

題意：給一個n（<=10）表示兩人手中共有n張牌，接下來一行表示第1個人有k1張牌，k1 v1[1] v1[2]......v1[k1], v1[i]表示第i 張牌的大小，第三行表示第2個人有k2張牌，k2 v2[1] v2[2]......v2[k2], v2[i]表示第i 張牌的大小。每一輪，兩人從牌頂部各出一張，誰出的牌大則兩張牌歸誰，放入到自己牌的底部，直到其中一個人手中沒有牌出，則那個人輸了。問需要多少輪，哪個人贏了。如果沒有解則輸出-1.

思路：（模擬題）直接模擬一下過程，主要是標記一下兩個人手中牌的狀態，用map<string,map<string,bool> >vist 標記一下。

轉載請注明出處：尋找&星空の孩子

題目鏈接：http://codeforces.com/contest/546/problem/C

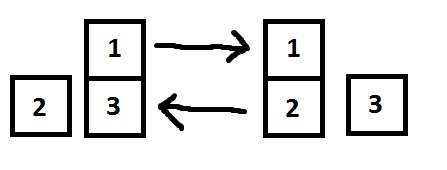
  1 #include <iostream>
  2 #include <stdio.h>
  3 #include <string.h>
  4 #include <string>
  5 #include <stack>
  6 #include <queue>
  7 #include <map>
  8 #include <set>
  9 #include <vector>
 10 #include <math.h>
 11 #include <bitset>
 12 #include <list>
 13 #include <algorithm>
 14 #include <climits>
 15 using namespace std;
 16 
 17 #define lson 2*i
 18 #define rson 2*i+1
 19 #define LS l,mid,lson
 20 #define RS mid+1,r,rson
 21 #define UP(i,x,y) for(i=x;i<=y;i++)
 22 #define DOWN(i,x,y) for(i=x;i>=y;i--)
 23 #define MEM(a,x) memset(a,x,sizeof(a))
 24 #define W(a) while(a)
 25 #define gcd(a,b) __gcd(a,b)
 26 #define LL long long
 27 #define N 5000005
 28 #define INF 0x3f3f3f3f
 29 #define EXP 1e-8
 30 #define lowbit(x) (x&-x)
 31 const int mod = 1e9+7;
 32 
 33 map<string,map<string,int> > vis;
 34 int n;
 35 int k1,k2;
 36 int a[15],b[15],c[15];
 37 char s1[15],s2[15];
 38 
 39 int main()
 40 {
 41     int i,j,k;
 42     scanf("%d",&n);
 43     scanf("%d",&k1);
 44     for(i = 0; i<k1; i++)
 45     {
 46         scanf("%d",&a[i]);
 47         c[i] = a[i];
 48     }
 49     scanf("%d",&k2);
 50     for(i = 0; i<k2; i++)
 51     {
 52         scanf("%d",&b[i]);
 53         c[k1+i] = b[i];
 54     }
 55     sort(c,c+k1+k2);
 56     for(i = 0; i<k1; i++)
 57     {
 58         for(j = 0; j<k1+k2; j++)
 59         {
 60             if(a[i]==c[j])
 61                 s1[i] = j+'0';
 62         }
 63     }
 64     s1[k1] = '\0';
 65     for(i = 0; i<k2; i++)
 66     {
 67         for(j = 0; j<k1+k2; j++)
 68         {
 69             if(b[i]==c[j])
 70                 s2[i] = j+'0';
 71         }
 72     }
 73     s2[k2] = '\0';
 74     vis[s1][s2] = 1;
 75     int ans = 0;
 76     while(k1&&k2)
 77     {
 78         int p1 = s1[0],p2 = s2[0];
 79       //  printf("[%d %d %d %d]\n",p1,p2,k1,k2);
 80 
 81         /* printf("(1):");
 82          for(i = 0; i<k1; i++)
 83              printf("%c ",s1[i]);
 84          printf("\n");
 85          printf("(2):");
 86          for(i = 0; i<k2; i++)
 87              printf("%c ",s2[i]);
 88          printf("\n");*/
 89         if(p1>p2)
 90         {
 91             for(i = 0; i<k2; i++)
 92                 s2[i] = s2[i+1];
 93             k2--;
 94             for(i = 0; i<k1; i++)
 95                 s1[i] = s1[i+1];
 96             s1[k1-1] = p2;
 97             s1[k1] = p1;
 98             k1++;
 99             s2[k2] = s1[k1] = '\0';
100         }
101         else
102         {
103             for(i = 0; i<k1; i++)
104                 s1[i] = s1[i+1];
105             k1--;
106             for(i = 0; i<k2; i++)
107                 s2[i] = s2[i+1];
108             s2[k2-1] = p1;
109             s2[k2] = p2;
110             k2++;
111             s2[k2] = s1[k1] = '\0';
112         }
113      /*   printf("(1):");
114         for(i = 0; i<k1; i++)
115             printf("%c ",s1[i]);
116         printf("\n");
117         printf("(2):");
118         for(i = 0; i<k2; i++)
119             printf("%c ",s2[i]);
120         printf("\n");*/
121         if(vis[s1][s2])
122         {
123             ans = -1;
124             break;
125         }
126         //printf("%d %d\n",k1,k2);
127         ans++;
128         vis[s1][s2] = 1;
129     }
130     printf("%d",ans);
131     if(ans!=-1)
132     {
133         if(k1)
134             printf(" 1");
135         else
136             printf(" 2");
137     }
138     printf("\n");
139 
140     return 0;
141 }

D. Soldier and Number Game

Two soldiers are playing a game. At the beginning first of them chooses a positive integer n and gives it to the second soldier. Then the second one tries to make maximum possible number of rounds. Each round consists of choosing a positive integer x > 1, such that n is divisible by x and replacing n with n / x. When n becomes equal to 1 and there is no more possible valid moves the game is over and the score of the second soldier is equal to the number of rounds he performed.

To make the game more interesting, first soldier chooses n of form a! / b! for some positive integer a and b (a ≥ b). Here by k! we denote the factorial of k that is defined as a product of all positive integers not large than k.

What is the maximum possible score of the second soldier?

Input

First line of input consists of single integer t (1 ≤ t ≤ 1 000 000) denoting number of games soldiers play.

Then follow t lines, each contains pair of integers a and b (1 ≤ b ≤ a ≤ 5 000 000) defining the value of n for a game.

Output

For each game output a maximum score that the second soldier can get.

Sample test(s) input

2
3 1
6 3

output

2
5

題意：n=a！/b！問你n的素數因子的個數。

思路：素數打表；

轉載請注明出處：尋找&星空の孩子

題目鏈接：http://codeforces.com/contest/546/problem/D

 1 #include <iostream>
 2 #include <stdio.h>
 3 #include <string.h>
 4 #include <string>
 5 #include <stack>
 6 #include <queue>
 7 #include <map>
 8 #include <set>
 9 #include <vector>
10 #include <math.h>
11 #include <bitset>
12 #include <list>
13 #include <algorithm>
14 #include <climits>
15 using namespace std;
16 
17 #define lson 2*i
18 #define rson 2*i+1
19 #define LS l,mid,lson
20 #define RS mid+1,r,rson
21 #define UP(i,x,y) for(i=x;i<=y;i++)
22 #define DOWN(i,x,y) for(i=x;i>=y;i--)
23 #define MEM(a,x) memset(a,x,sizeof(a))
24 #define W(a) while(a)
25 #define gcd(a,b) __gcd(a,b)
26 #define LL long long
27 #define N 5000005
28 #define INF 0x3f3f3f3f
29 #define EXP 1e-8
30 #define lowbit(x) (x&-x)
31 const int mod = 1e9+7;
32 int p[N];
33 int a[N];
34 int prime[700];
35 LL sum[N];
36 void init()
37 {
38 
39     for(int i=0; i<700; ++i)
40         prime[i] = INF;
41     prime[0] = 2;
42     int num = 0;
43     for(int i=3; i<5005; ++i)
44     {
45         int x = 0;
46         while(i%prime[x] && prime[x] <= i)   ++x;
47         if( !(i%prime[x]) )
48             a[i] = prime[x];
49         else
50         {
51             prime[++num] = i;
52             a[i] = i;
53         }
54     }
55     a[2] =2;
56     for(int i=5005; i< N; ++i)
57     {
58         int x = 0;
59         while(i%prime[x] && prime[x] <= i)   ++x;
60         if( !(i%prime[x]) )
61             a[i] = prime[x];
62         else
63             a[i] = i;
64     }
65     p[2] = 1;
66     for(int i=3; i <N; ++i)
67         p[i] = p[i/a[i]] + 1;
68 }
69 int main()
70 {
71     int i,j,k;
72     init();
73     sum[1] = 0;
74    // printf("%d\n",p[4]);
75     for(i = 2; i<=5000000; i++)
76     {
77         sum[i] = sum[i-1]+p[i];
78       //  printf("%d %I64d\n",i,sum[i]);
79     }
80     int t;
81     scanf("%d",&t);
82     while(t--)
83     {
84         scanf("%d%d",&i,&j);
85        // printf("%d %d %I64d %I64d\n",i,j+1,sum[i],sum[j+1]);
86         if(i == j)
87             printf("0\n");
88         else
89             printf("%I64d\n",sum[i]-sum[j]);
90     }
91 
92     return 0;
93 }

 1 #include <iostream>
 2 #include <stdio.h>
 3 #include <string.h>
 4 #include <string>
 5 #include <stack>
 6 #include <queue>
 7 #include <map>
 8 #include <set>
 9 #include <vector>
10 #include <math.h>
11 #include <bitset>
12 #include <list>
13 #include <algorithm>
14 #include <climits>
15 using namespace std;
16 
17 #define lson 2*i
18 #define rson 2*i+1
19 #define LS l,mid,lson
20 #define RS mid+1,r,rson
21 #define UP(i,x,y) for(i=x;i<=y;i++)
22 #define DOWN(i,x,y) for(i=x;i>=y;i--)
23 #define MEM(a,x) memset(a,x,sizeof(a))
24 #define W(a) while(a)
25 #define gcd(a,b) __gcd(a,b)
26 #define LL long long
27 #define N 5000005
28 #define INF 0x3f3f3f3f
29 #define EXP 1e-8
30 #define lowbit(x) (x&-x)
31 const int mod = 1e9+7;
32 int p[N];
33 bool v[N]; 
34 int a[N];
35 int prime[N/10];
36 LL sum[N];
37 void init()
38 {
39     for(int i=2; i<N; ++i)
40         a[i] = i;
41     int num=-1;
42     for(int i=2; i<N; ++i)
43     {
44         if(!v[i]) prime[++num] = i;
45         for(int j=0; j<=num && i*prime[j] < N; ++j)
46         {
47             int t = i*prime[j];
48             v[t] =1;
49             if(a[t] > prime[j]) a[t] = prime[j];
50             if(i%prime[j] == 0) break;
51         }
52     }
53     p[2] = 1;
54     for(int i=3; i <N; ++i)
55         p[i] = p[i/a[i]] + 1;
56 }
57 int main()
58 {
59     int i,j,k;
60     init();
61     sum[1] = 0;
62     for(i = 2; i<=5000000; i++)
63     {
64         sum[i] = sum[i-1]+p[i];
65     }
66     int t;
67     scanf("%d",&t);
68     while(t--)
69     {
70         scanf("%d%d",&i,&j);
71         if(i == j)
72             printf("0\n");
73         else
74             printf("%I64d\n",sum[i]-sum[j]);
75     }
76 
77     return 0;
78 }

E. Soldier and Traveling

In the country there are n cities and m bidirectional roads between them. Each city has an army. Army of the i-th city consists of aisoldiers. Now soldiers roam. After roaming each soldier has to either stay in his city or to go to the one of neighboring cities by at moving along at most one road.

Check if is it possible that after roaming there will be exactly bi soldiers in the i-th city.

Input

First line of input consists of two integers n and m (1 ≤ n ≤ 100, 0 ≤ m ≤ 200).

Next line contains n integers a1, a2, ..., an (0 ≤ ai ≤ 100).

Next line contains n integers b1, b2, ..., bn (0 ≤ bi ≤ 100).

Then m lines follow, each of them consists of two integers p and q (1 ≤ p, q ≤ n, p ≠ q) denoting that there is an undirected road between cities p and q.

It is guaranteed that there is at most one road between each pair of cities.

Output

If the conditions can not be met output single word "NO".

Otherwise output word "YES" and then n lines, each of them consisting of n integers. Number in the i-th line in the j-th column should denote how many soldiers should road from city i to city j (if i ≠ j) or how many soldiers should stay in city i (if i = j).

If there are several possible answers you may output any of them.

Sample test(s) input

output

input

2 0
1 2
2 1

output

NO

題意：給你一張無向圖，每個點有一定數量的人，通過移動可以去鄰接點（但是只能移動一次）問你是否能從初始狀態移動到目標狀態；

思路:網絡流+最大流；

轉載請注明出處：尋找&星空の孩子

題目鏈接：http://codeforces.com/contest/546/problem/E

  1 #include<stdio.h>
  2 #include<string.h>
  3 #include<queue>
  4 #include<algorithm>
  5 using namespace std;
  6 #define captype int
  7 
  8 const int MAXN = 510;   //點的總數
  9 const int MAXM = 400010;    //邊的總數
 10 const int INF = 1<<30;
 11 struct EDG{
 12     int to,next;
 13     captype cap,flow;
 14 } edg[MAXM];
 15 int eid,head[MAXN];
 16 int gap[MAXN];  //每種距離(或可認為是高度)點的個數
 17 int dis[MAXN];  //每個點到終點eNode 的最短距離
 18 int cur[MAXN];  //cur[u] 表示從u點出發可流經 cur[u] 號邊
 19 int pre[MAXN];
 20 int mapt[105][105];
 21 
 22 void init(){
 23     eid=0;
 24     memset(head,-1,sizeof(head));
 25     memset(mapt,0,sizeof(mapt));
 26 }
 27 //有向邊 三個參數，無向邊4個參數
 28 void addEdg(int u,int v,captype c,captype rc=0){
 29     edg[eid].to=v; edg[eid].next=head[u];
 30     edg[eid].cap=c; edg[eid].flow=0; head[u]=eid++;
 31 
 32     edg[eid].to=u; edg[eid].next=head[v];
 33     edg[eid].cap=rc; edg[eid].flow=0; head[v]=eid++;
 34 }
 35 captype maxFlow_sap(int sNode,int eNode, int n){//n是包括源點和匯點的總點個數，這個一定要注意
 36     memset(gap,0,sizeof(gap));
 37     memset(dis,0,sizeof(dis));
 38     memcpy(cur,head,sizeof(head));
 39     pre[sNode] = -1;
 40     gap[0]=n;
 41     captype ans=0;  //最大流
 42     int u=sNode;
 43     while(dis[sNode]<n){   //判斷從sNode點有沒有流向下一個相鄰的點
 44         if(u==eNode){   //找到一條可增流的路
 45             captype Min=INF ;
 46             int inser;
 47             for(int i=pre[u]; i!=-1; i=pre[edg[i^1].to])    //從這條可增流的路找到最多可增的流量Min
 48             if(Min>edg[i].cap-edg[i].flow){
 49                 Min=edg[i].cap-edg[i].flow;
 50                 inser=i;
 51             }
 52             for(int i=pre[u]; i!=-1; i=pre[edg[i^1].to]){
 53 
 54                 edg[i].flow+=Min;
 55                 edg[i^1].flow-=Min;  //可回流的邊的流量
 56                 
 57                 if(edg[i].to==eNode||edg[i].to==sNode||edg[i^1].to==eNode||edg[i^1].to==sNode)
 58                     continue;
 59                 if(edg[i].cap>0){
 60                     int tu, tv;
 61                     tu=edg[i^1].to; tv=edg[i].to-(n-1)/2;
 62                     mapt[tu][tv]+=Min;
 63                 }
 64                 else{
 65                     int tu, tv;
 66                     tu=edg[i].to; tv=edg[i^1].to-(n-1)/2;
 67                     mapt[tu][tv]-=Min;
 68                 }
 69                 
 70             }
 71             ans+=Min;
 72             u=edg[inser^1].to;
 73             continue;
 74         }
 75         bool flag = false;  //判斷能否從u點出發可往相鄰點流
 76         int v;
 77         for(int i=cur[u]; i!=-1; i=edg[i].next){
 78             v=edg[i].to;
 79             if(edg[i].cap-edg[i].flow>0 && dis[u]==dis[v]+1){
 80                 flag=true;
 81                 cur[u]=pre[v]=i;
 82                 break;
 83             }
 84         }
 85         if(flag){
 86             u=v;
 87             continue;
 88         }
 89         //如果上面沒有找到一個可流的相鄰點，則改變出發點u的距離（也可認為是高度）為相鄰可流點的最小距離+1
 90         int Mind= n;
 91         for(int i=head[u]; i!=-1; i=edg[i].next)
 92         if(edg[i].cap-edg[i].flow>0 && Mind>dis[edg[i].to]){
 93             Mind=dis[edg[i].to];
 94             cur[u]=i;
 95         }
 96         gap[dis[u]]--;
 97         if(gap[dis[u]]==0) return ans;  //當dis[u]這種距離的點沒有了，也就不可能從源點出發找到一條增廣流路徑
 98                                         //因為匯點到當前點的距離只有一種，那麼從源點到匯點必然經過當前點，然而當前點又沒能找到可流向的點，那麼必然斷流
 99         dis[u]=Mind+1;//如果找到一個可流的相鄰點，則距離為相鄰點距離+1，如果找不到，則為n+1
100         gap[dis[u]]++;
101         if(u!=sNode) u=edg[pre[u]^1].to;  //退一條邊
102     }
103     return ans;
104 }
105 int main(){
106     int n,m ,s , t , u,v,c[105],tc;
107     while(scanf("%d%d",&n,&m)>0){
108         init();
109         s=0;
110         t=2*n+1;
111         int ans=0;
112         for(int i=1; i<=n; i++){
113             scanf("%d",&c[i]);
114             ans+=c[i];
115             addEdg(s,i,c[i]);
116             addEdg(i,i+n,c[i]);
117         }
118         int sum=0;
119         for(int i=1; i<=n; i++)
120         {
121             scanf("%d",&tc); sum+=tc;
122             addEdg(i+n,t,tc);
123         }
124         while(m--){
125             scanf("%d%d",&u,&v);
126             addEdg(u,v+n,c[u]);
127             addEdg(v,u+n,c[v]);
128         }
129         if(ans!=sum){
130             printf("NO\n"); continue;
131         }
132         ans -= maxFlow_sap(s,t,t+1);
133         if(ans==0){
134             printf("YES\n");
135             for(int i=1; i<=n; i++){
136                 for(int j=1; j<n; j++)
137                     printf("%d ",mapt[i][j]);
138                 printf("%d\n",mapt[i][n]);
139             }
140         }
141         else
142             printf("NO\n");
143     }
144 }