sgu251：Polymania(構造)
題目大意：
給出平面上n(3≤n≤8)個點，每個點有一個坐標(未知)和正整數權值Ri，其中Rn?1=Rn，給出一組坐標構造，使得任意三個點構成的三角形面積為這三個點的權值和。
分析：
我們以最後兩個有相等權值的點為基來考慮。
滿足條件的一組構造必定滿足如下條件：
1.因為權值均為正整數，所以沒有三點共線；
2.構造必定形如：
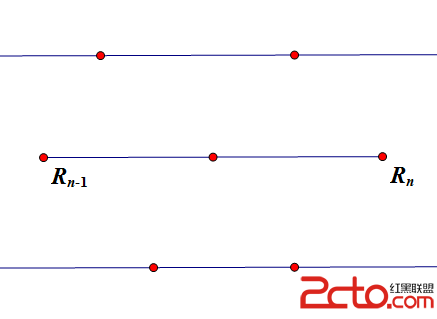vcz1xr3Q0M/fyc+31rHwyM7IodK7uPa146Os1eLBvbj2tePBrM/fts6x2Ln9PG5vYnI+Um4/MSxSbjwvbm9icj61xNbQteOhozxiciAvPg0KPG5vYnI+IDwvbm9icj7X28nPy/nK9qOstbE8bm9icj5uJmd0OzQ8L25vYnI+yrGjrNK7tqjO3r3io7s8YnIgLz4NCjxub2JyPiA8L25vYnI+tbE8bm9icj5uPTQ8L25vYnI+yrGjrMj0PG5vYnI+UjErUjI9UjMrUjQ8L25vYnI+o6zEx8O0v8nS1LDRPG5vYnI+UjEsUjI8L25vYnI+yc/PwrfFo7s8YnIgLz4NCjxub2JyPiA8L25vYnI+yPQ8bm9icj5SMT1SMjwvbm9icj6jrL/J0tTBvbj2try3xcnPw+ajuzxiciAvPg0KPG5vYnI+IDwvbm9icj638dTyzt694qO7PGJyIC8+DQo8bm9icj4gPC9ub2JyPrWxPG5vYnI+bj0zPC9ub2JyPsqxo6zSu7ao09C94qOsy+ax47m51Oy8tL/JoaM8L3A+DQo8cD5BQyBjb2Rlo7o8L3A+DQo8cHJlIGNsYXNzPQ=="brush:java;">
#include
#include
typedef double DB;
using namespace std;
const int MAXN = 5;
const DB eps = 1e-8;
int n;
DB a[MAXN];
int main()
{
#ifndef ONLINE_JUDGE
freopen("input.txt", "r", stdin);
freopen("output.txt", "w", stdout);
#endif
scanf("%d", &n);
if(n > 4) puts("NO");
else
{
for(int i = 1; i <= n; ++i)
scanf("%lf", a+i);
if(n == 4)
{
if(fabs(a[1]+a[2]-a[3]-a[4]) > eps)
{
if(fabs(a[1]-a[2]) > eps) puts("NO");
else
{
DB x3 = -10, x4 = 10, x, y;
y = (a[1]+a[3]+a[4])*2/(x4-x3);
x = (a[1]+a[2]+a[3])*2/y;
puts("YES");
printf("%.4lf %.4lf\n", -x/2, y);
printf("%.4lf %.4lf\n", x/2, y);
printf("%.4lf 0.0000\n", x3);
printf("%.4lf 0.0000\n", x4);
}
}
else
{
DB x3 = -10, x4 = 10, y1, y2;
y1 = (a[1]+a[3]+a[4])*2/(x4-x3);
y2 = -(a[2]+a[3]+a[4])*2/(x4-x3);
puts("YES");
printf("0.0000 %.4lf\n", y1);
printf("0.0000 %.4lf\n", y2);
printf("%.4lf 0.0000\n", x3);
printf("%.4lf 0.0000\n", x4);
}
}
else
{
DB x2 = -10, x3 = 10, y1;
y1 = (a[1]+a[2]+a[3])*2/(x3-x2);
puts("YES");
printf("0.0000 %.4lf\n", y1);
printf("%.4lf 0.0000\n", x2);
printf("%.4lf 0.0000\n", x3);
}
}
#ifndef ONLINE_JUDGE
fclose(stdin);
fclose(stdout);
#endif
return 0;
}
