hihocoder #1042 : 跑馬圈地

hihocoder #1042 : 跑馬圈地

描述

一覺醒來，小Hi穿越回了古代！由於破敵有功，大汗賞賜小Hi可以在敵人的草原上跑馬圈地：一天之內騎馬圍住的草原以後就是小Hi的牧場。但是令小Hi頭疼的是，敵人的草原上有一塊臭水塘。小Hi不能騎馬走進臭水塘裡，並且即使小Hi的騎馬路徑圍住了臭水塘，小Hi的牛馬也不能在臭水塘裡放牧。

為了更科學地圈地，小Hi對這個問題進行了簡化和抽象：(1)敵人的草原是一塊n×m的方格矩陣，(2)騎馬的路徑是沿著方格邊緣的一段封閉折線，(3)臭水塘是矩陣中的一塊矩形，(4)騎馬的路徑周長不超過L。小Hi想知道自己最大能圈住多大面積的草原(臭水塘的面積不計入在內)。

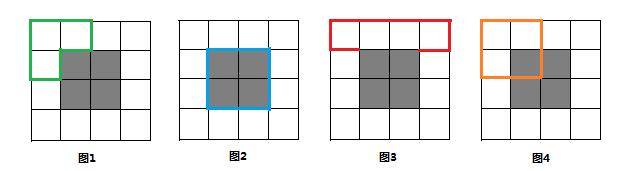
如圖所示：圖1是一條合法的路徑；圖2也是一條合法的路徑，但是圈住的草原面積為0；圖3不是合法的路徑，因為沒有封閉；圖4也不是合法的路徑，因為穿過了水塘。

輸入

第一行3個整數：n, m, L (1 <= n, m <= 100, 1 <= L <= 400)

第二行4個整數：l, r, t, b (0 <= l < r <= m, 0 <= t < b <= n)表示水塘的左、右、上、下邊界坐標。

輸出

小Hi最大能圈住的面積

樣例輸入

4 4 8
1 3 1 3

樣例輸出

3

 

很顯然L越大覆蓋的面積就越大，所以這題應該是周長取L時枚舉所有的面積。

主要是考慮一下三種情況：

1.圈地與水塘沒有重疊部分

2.水塘的一個頂點在圈地內

3.水塘的四個頂點都在圈地內

 

可以通過坐標變換，把水塘都變成位於草原右上角的情況。

根據水塘中心的坐標來判斷水塘是位於左上、右上、左下還是右下。

 

對於水塘坐標的轉換

 

int l1, r1, t1, b1;
	if (l + r <= m &&t + b <= n)   //左下角
	{
		l1 = m - r;
		r1 = m - l;
		t1 = n - b;
		b1 = n - t;
	}
	else if (l + r >= m &&t + b <= n)  //右下角
	{
		l1 = l;
		r1 = r;
		t1 = n - b;
		b1 = n - t;
	}
	else if (l + r <= m &&t + b >= n)  //左上角
	{
		l1 = m - r;
		r1 = m - l;
		t1 = t;
		b1 = b;
	}

可以簡化成：

 

 

int l1, r1, t1, b1;
	l1 = l;
	r1 = r;
	t1 = t;
	b1 = b;
	if (l + r <= m)   
	{
		l1 = m - r;
		r1 = m - l;
	}
	if (t + b <= n)
	{
		t1 = n - b;
		b1 = n - t;
	}

完整程序如下：

 

 

#include 
using namespace std;

int main()
{
	int n, m, L, l, r, t, b;
	cin >> n >> m >> L;
	cin >> l >> r >> b >> t;
	if (L >= 2 * (m + n))
	{
		cout << m*n - (r - l)*(t - b) << endl;
		return 0;
	}
	int l1, r1, t1, b1;
	l1 = l;
	r1 = r;
	t1 = t;
	b1 = b;
	if (l + r <= m)   
	{
		l1 = m - r;
		r1 = m - l;
	}
	if (t + b <= n)
	{
		t1 = n - b;
		b1 = n - t;
	}
	int ans = 0;
	for (int i = 1; i < L / 2 && i <= m; i++)
	{
		for (int j = 1; j <= L / 2 - i&&j <= n; j++)
		{
			if (i <= l1 || j <= b1)
				ans = ans >i*j ? ans : i*j;
			else if (i > l1 && i <= r1 && j > b1 && j <= t1)
				ans = ans > i*j - (i - l1)*(j - b1) ? ans : i*j - (i - l1)*(j - b1);
			else if (i >= r1&&j >= t1)
				ans = ans > i*j - (r - l)*(t - b) ? ans : i*j - (r - l)*(t - b);
			else
				continue;
		}
	}

	cout << ans << endl;
	system(pause);

	return 0;
}

 

(づ￣ 3￣)づ