hihocoder #1083 : 積分

hihocoder #1083 : 積分

描述

在平面上有一個頂點數為N的多邊形P，區域

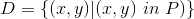
你需要寫一個程序計算這個積分

輸入

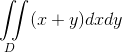
輸入包含T (T<=500)個測試用例。數字T在輸入文件的第一行給出。每個測試用例的第一行是一個整數N代表多邊形的點數。其後跟隨N行，每行包含兩個點Xi和Yi，表示第i個點的坐標，當我們以給定的順序連接這些點，我們得到了一個多邊形。題目保證多邊形不自交，這個多邊形的面積也不會是零，也不會出現3個相鄰的點共線的情況。

【參數說明】

3 <= N <= 8000

|Xi|, |Yi| <= 20000

輸出

對於每個測試用例行輸出結果占一行。將答案四捨五入到小數點後兩位（0.005四捨五入到0.01）。

樣例輸入

2
4
4 -1
-1 4
-6 -1
-1 -6
4
0 0
10 0
10 10
0 10

樣例輸出

-100.00
1000.00

 

為了做這題逼得我把積分看了一下，想到上次做微積分還是很久遠的事情。

知道怎麼求任意凸多邊形的重心麼~鏈接拿好http://wenku.baidu.com/view/1e0c290bf78a6529647d53f2.html

概括一下怎麼求重心：

在物理中重心的求法是：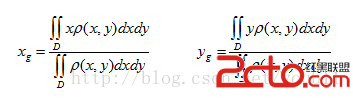

在數學上密度是均勻的，所以密度函數可以看成常量，約去後得到：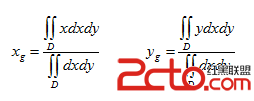

而且

 

發現題目要求的東西可以變成這樣：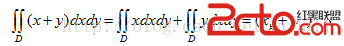

 

對於無規則的凸多邊形，以某個固定的頂點向其他頂點劃線，可以把這個凸多邊形分成多個三角形的組合。

然後這個題目就分解成了求多個三角形的重心坐標以及三角形的面積。

利用三角形個頂點坐標求解三角形面積的辦法：叉乘

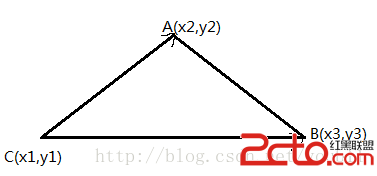
面積為S=|CA向量叉乘CB向量|/2=|(x2-x1)*(y3-y1)-(y2-x1)*(x3-x1)|/2

 

 

 

#include 
#include 
using namespace std;

double x[8005], y[8005];

int main() 
{
	int T, n;
	cin >> T;
	while(T--) 
	{
		cin >> n;
		for (int i = 0; i < n;i++)
			cin >> x[i] >> y[i];

		double ans = 0;
		double small_s;
		double S = 0;
		for (int i = 2; i < n; i++)
		{
			small_s = ((x[i - 1] - x[0])*(y[i] - y[0]) - (y[i - 1] - y[0])*(x[i] - x[0])) / 2.0;
			S += small_s;
			double xg = (x[i - 1] + x[0] + x[i]) / 3.0;
			double yg = (y[i - 1] + y[0] + y[i]) / 3.0;
			ans += (xg + yg)*small_s;
		}
		if (S < 0)
			ans = -ans;
		
		cout << fixed << setprecision(2) << ans << endl;
	}
	
	system("pause");
	return 0;
}