我們把集合: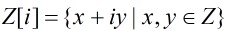 叫做高斯整數環,其中Z表示通常的整數環,而用
叫做高斯整數環,其中Z表示通常的整數環,而用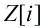 表示復數域上的整數環。
表示復數域上的整數環。
那麼什麼是環呢?就是通過加減乘三種運算後,仍然能滿足本身性質的就叫做環。
范的定義:設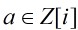 ,
,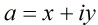 ,定義a的范為
,定義a的范為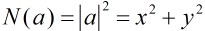
設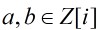 ,則
,則
(1)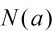 為非負整數,並且
為非負整數,並且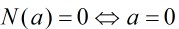
(2)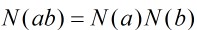
(3)若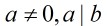 ,則
,則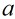
逆的定義:設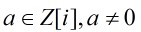 ,如果存在
,如果存在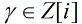 ,使得
,使得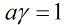 ,則稱
,則稱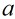 為
為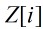 中的乘法可逆元,簡稱可逆元,並且
中的乘法可逆元,簡稱可逆元,並且
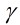 叫做
叫做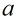 的逆。
的逆。
高斯整數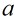 是可逆元的充要條件是:
是可逆元的充要條件是: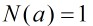 。
。 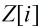 中只有4個可逆元,分別是:
中只有4個可逆元,分別是: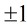 和
和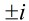
定義:設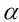 和
和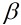 是兩個非零高斯整數,如果存在可逆元
是兩個非零高斯整數,如果存在可逆元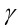 ,使得
,使得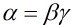 ,則稱
,則稱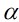 和
和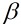 等價,並表示成
等價,並表示成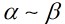 ,換句話說,
,換句話說,
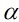 與
與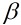 等價,是指
等價,是指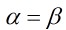 ,
,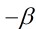 ,
,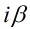 或者
或者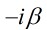
高斯素數
定義:設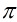 為
為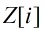 中的非零非可逆元,我們稱
中的非零非可逆元,我們稱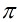 為高斯素數,是指
為高斯素數,是指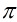 的每個因子或者為可逆元,或者是與
的每個因子或者為可逆元,或者是與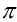 等價的高斯整數。
等價的高斯整數。
引理:
(1)設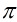 為高斯整數,並且
為高斯整數,並且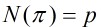 為素數,則
為素數,則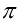 必定為高斯素數。
必定為高斯素數。
(2)若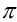 為高斯素數,則其共轭元
為高斯素數,則其共轭元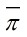 也是高斯素數。
也是高斯素數。
如何判斷一個高斯整數是否屬於高斯素數呢?可以用下面的方法:
高斯整數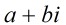 是素數當且僅當:
是素數當且僅當:
(1)a、b中有一個是零,另一個數的絕對值是形如4n+3的素數;
(2)a、b均不為零,而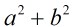 為素數;
為素數;
有了這個結論,那麼我們就可以很輕松的解決HDU2650題了。
題目:A math problem
題意:給出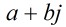 ,其中
,其中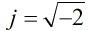 ,判斷
,判斷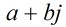 是否為高斯素數。
是否為高斯素數。
分析:其實就是上面的判斷高斯素數的方法,但是注意一點,這裡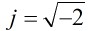 ,而正常情況是
,而正常情況是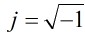 ,其實差不多一樣,
,其實差不多一樣,
只是把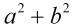 為素數這個條件改為:
為素數這個條件改為: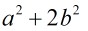 為素數即可,那麼如果把題目描述改為
為素數即可,那麼如果把題目描述改為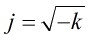 呢?同樣的道理只需把
呢?同樣的道理只需把
判斷條件改成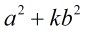 為素數即可,由於
為素數即可,由於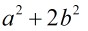 很大,所以寫個Miller_Rabin吧。。。
很大,所以寫個Miller_Rabin吧。。。
import java.text.DecimalFormat;
import java.util.ArrayDeque;
import java.io.BufferedReader;
import java.io.InputStreamReader;
import java.io.PrintWriter;
import java.math.BigInteger;
import java.util.ArrayList;
import java.util.Arrays;
import java.util.Collections;
import java.util.Comparator;
import java.util.Deque;
import java.util.HashMap;
import java.util.Iterator;
import java.util.LinkedList;
import java.util.Map;
import java.util.PriorityQueue;
import java.util.Random;
import java.util.Scanner;
import java.util.Stack;
import java.util.StringTokenizer;
import java.util.TreeMap;
import java.util.TreeSet;
import java.util.Queue;
import java.io.File;
import java.io.FileInputStream;
import java.io.FileNotFoundException;
import java.io.FileOutputStream;
public class Main{
long multi(long a,long b,long m)
{
long ans=0;
while(b>0)
{
if((b&1)!=0)
{
ans=(ans+a)%m;
b--;
}
b/=2;
a=(a+a)%m;
}
return ans;
}
long quick_mod(long a,long b,long m)
{
long ans=1;
a%=m;
while(b>0)
{
if((b&1)!=0)
{
ans=multi(ans,a,m);
b--;
}
b/=2;
a=multi(a,a,m);
}
return ans;
}
boolean MillarRabin(long n)
{
if(n==2) return true;
if(n<2||0==(n&1)) return false;
long a,m=n-1,x,y = 0;
int k=0;
while((m&1)==0)
{
k++;
m/=2;
}
for(int i=0;i<10;i++)
{
a=abs(rand.nextLong())%(n-1)+1;
x=quick_mod(a,m,n);
for(int j=0;j> 1;
if (A[mid] <= val) {
l = mid + 1;
} else {
pos = mid;
r = mid - 1;
}
}
return pos;
}
int Pow(int x, int y) {
int ans = 1;
while (y > 0) {
if ((y & 1) > 0)
ans *= x;
y >>= 1;
x = x * x;
}
return ans;
}
double Pow(double x, int y) {
double ans = 1;
while (y > 0) {
if ((y & 1) > 0)
ans *= x;
y >>= 1;
x = x * x;
}
return ans;
}
int Pow_Mod(int x, int y, int mod) {
int ans = 1;
while (y > 0) {
if ((y & 1) > 0)
ans *= x;
ans %= mod;
y >>= 1;
x = x * x;
x %= mod;
}
return ans;
}
long Pow(long x, long y) {
long ans = 1;
while (y > 0) {
if ((y & 1) > 0)
ans *= x;
y >>= 1;
x = x * x;
}
return ans;
}
long Pow_Mod(long x, long y, long mod) {
long ans = 1;
while (y > 0) {
if ((y & 1) > 0)
ans *= x;
ans %= mod;
y >>= 1;
x = x * x;
x %= mod;
}
return ans;
}
int Gcd(int x, int y){
if(x>y){int tmp = x; x = y; y = tmp;}
while(x>0){
y %= x;
int tmp = x; x = y; y = tmp;
}
return y;
}
long Gcd(long x, long y){
if(x>y){long tmp = x; x = y; y = tmp;}
while(x>0){
y %= x;
long tmp = x; x = y; y = tmp;
}
return y;
}
int Lcm(int x, int y){
return x/Gcd(x, y)*y;
}
long Lcm(long x, long y){
return x/Gcd(x, y)*y;
}
int max(int x, int y) {
return x > y ? x : y;
}
int min(int x, int y) {
return x < y ? x : y;
}
double max(double x, double y) {
return x > y ? x : y;
}
double min(double x, double y) {
return x < y ? x : y;
}
long max(long x, long y) {
return x > y ? x : y;
}
long min(long x, long y) {
return x < y ? x : y;
}
int abs(int x) {
return x > 0 ? x : -x;
}
double abs(double x) {
return x > 0 ? x : -x;
}
long abs(long x) {
return x > 0 ? x : -x;
}
boolean zero(double x) {
return abs(x) < eps;
}
double sin(double x){return Math.sin(x);}
double cos(double x){return Math.cos(x);}
double tan(double x){return Math.tan(x);}
double sqrt(double x){return Math.sqrt(x);}
}