UVA 1347(POJ 2677)Tour(雙調歐幾裡得旅行商問題)

UVA 1347(POJ 2677)Tour(雙調歐幾裡得旅行商問題)

Tour

Time Limit:3000MS Memory Limit:0KB 64bit IO Format:%lld & %llu

Description

John Doe, a skilled pilot, enjoys traveling. While on vacation, he rents a small plane and starts visiting beautiful places. To save money, John must determine the shortest closed tour that connects his destinations. Each destination is represented by a point in the plane p_i = < x_i, y_i > . John uses the following strategy: he starts from the leftmost point, then he goes strictly left to right to the rightmost point, and then he goes strictly right back to the starting point. It is known that the points have distinct x -coordinates.

Write a program that, given a set of n points in the plane, computes the shortest closed tour that connects the points according to John's strategy.

Input

The program input is from a text file. Each data set in the file stands for a particular set of points. For each set of points the data set contains the number of points, and the point coordinates in ascending order of the x coordinate. White spaces can occur freely in input. The input data are correct.

Output

For each set of data, your program should print the result to the standard output from the beginning of a line. The tour length, a floating-point number with two fractional digits, represents the result.

Note: An input/output sample is in the table below. Here there are two data sets. The first one contains 3 points specified by their x and y coordinates. The second point, for example, has the x coordinate 2, and the y coordinate 3. The result for each data set is the tour length, (6.47 for the first data set in the given example).

Sample Input

3 
1 1
2 3
3 1
4 
1 1 
2 3
3 1
4 2

Sample Output

6.47
7.89

題意：典型的動態規劃例題。又叫做雙調歐幾裡得旅行商問題。算法導論裡面的題目。

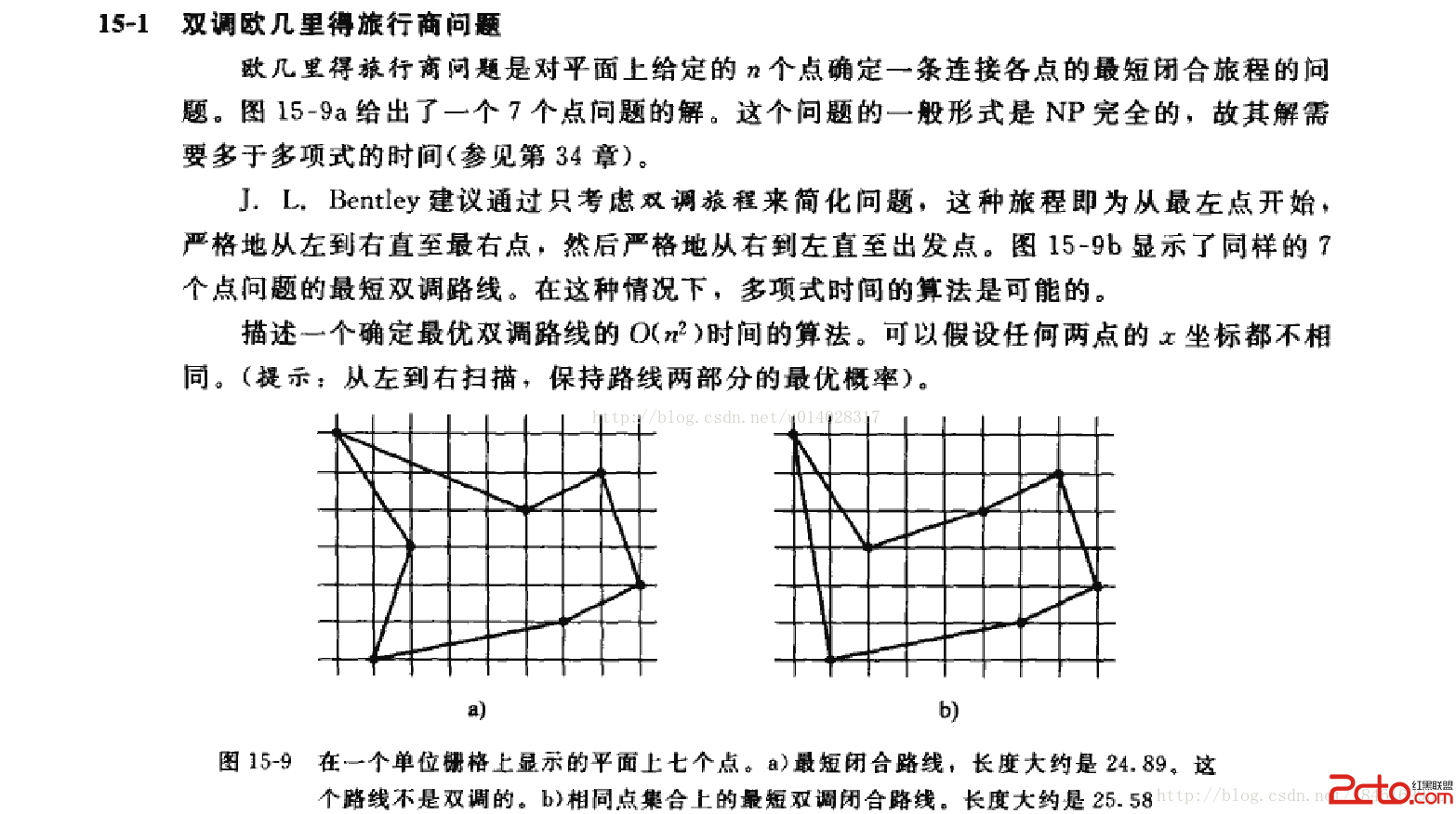
思路：

dp[i][j] 表示從 i 到 1，再從1到j的距離。在這個路徑上，點 1 到 Pmax(i,j) 點之間的所有點有且僅有經過一次。

dp[i][j] = dp[i-1][j] + dis(i,i-1);

dp[i][i-1] = min (dp[i][i-1], dp[i-1][j] + dis(i, j));

#include 
#include 
#include 
#include 
#include 
#include 
#include 
#include 
using namespace std;

const int INF = 1<<29;
const int MAXN = 1100;
const double PI = acos(-1.0);
const double e = 2.718281828459;
const double eps = 1e-8;
struct node
{
    double x;
    double y;
}a[MAXN];
double dp[MAXN][MAXN];

int cmp(node a, node b)
{
    return a.x < b.x;
}

double dist(int i, int j)
{
    return sqrt((a[i].x-a[j].x)*(a[i].x-a[j].x)+(a[i].y-a[j].y)*(a[i].y-a[j].y));
}

int main()
{
    //freopen("in.txt", "r", stdin);
    //freopen("out.txt", "w", stdout);
    int n;
    while(cin>>n)
    {
        for(int i = 1; i <= n; i++)
        {
            scanf("%lf %lf", &a[i].x, &a[i].y);
        }
        sort(a+1, a+1+n, cmp);
        dp[2][1] = dist(1, 2);
        for(int i = 3; i <= n; i++)
        {
            dp[i][i-1] = INF*1.0;
            for(int j = 1; j < i-1; j++)
            {
                dp[i][i-1] = min(dp[i][i-1], dp[i-1][j]+dist(i, j));
                dp[i][j] = dp[i-1][j]+dist(i-1, i);
            }
        }
        double ans = INF*1.0;
        for(int i = 1; i < n; i++)
        {
            ans = min(ans, dp[n][i]+dist(n, i));
        }
        printf("%.2f\n", ans);
    }
    return 0;
}