ZZULIOJ 1726: 迷宮

ZZULIOJ 1726: 迷宮

Description

在很多 RPG (Role-playing Games) 游戲中，迷宮往往是非常復雜的游戲環節。通常來說，我們在走迷宮的時候都需要花非常多的時間來嘗試不同的路徑。但如果有了算法和計算機的幫助，我們能不能有更快的方式來解決這個問題？我們可以進行一些嘗試。

現在我們有一個 N 行 M 列的迷宮。迷宮的每個格子如果是空地則可以站人，如果是障礙則不行。在一個格子上，我們可以一步移動到它相鄰的 8 個空地上，但不能離開地圖的邊界或者跨過兩個障礙的夾縫。下圖是一個移動規則的示例。

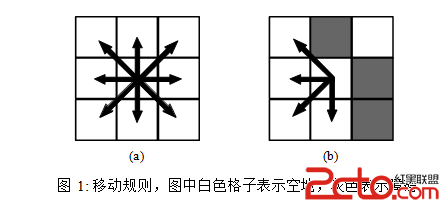
為了離開迷宮，我們還需要觸發迷宮中所有的機關。迷宮裡總共有 K 個機關，每個機關都落在一個不同的空地上。如果我們到達了某個機關所在的格子時，這個機關就會被自動觸發，並在觸發之後立即消失。我們的目標是按順序觸發所有的 K 個機關，而當最後一個機關被觸發時，我們就可以離開迷宮了。

現在我們已經拿到了迷宮地圖，並且知道所有障礙、機關的位置。初始時我們位於迷宮的某個非障礙格子上，請你計算我們最少需要移動多少步才能離開迷宮？

Input

輸入的第一行是測試數據的組數 T (T ≤ 20)。

對於每組測試數據：第一行包含地圖的行數 N (2 ≤ N ≤ 100)，列數 M(2 ≤ M ≤ 100) 和機關的數量 K(1 ≤ K ≤10)。接下來 N 行，每行包含 M 個字符，其中字符 ‘#’ 表示障礙，而 ‘.’ 表示空地。接下來一行描述了我們的初始位置 (x, y)，表示我們一開始在第 x 行第 y 列的格子上。這個格子保證是個空地。接下來 K 行，每行給出了一個機關的位置。所有的機關都不會出現在障礙上，並且任意兩個機關不會出現在同一個空地上。我們需要按輸入給定的順序觸發所有的 K 個機關。

Output

對於每組測試數據，輸出離開迷宮所需要的最少步數。如果無論如何都不能離開迷宮，輸出 -1。

Sample Input

Sample Output

坑是起點為第二個或以後的機關上。

#include 
#include 
#include 
#include 

using namespace std;

const int maxn = 110;
const int inf = 0x3f3f3f3f;
const int dir[][2] = {0, 1, 0, -1, -1, 0, 1, 0, 1, 1, 1, -1, -1, 1, -1, -1};
char G[maxn][maxn];
bool vis[maxn][maxn];
int N, M, K; // N rows
int sx, sy, tx, ty;
vector vec;
struct Node {
    int x, y, step;
};

void getMap()
{
    int i, j, x, y;
    for (i = 1; i <= N; ++i)
        scanf("%s", G[i] + 1);
    scanf("%d%d", &sx, &sy);

    vec.clear();

    for (i = 0; i < K; ++i) {
        cin >> x >> y;
        G[x][y] = '@';
        vec.push_back(x);
        vec.push_back(y);
    }
}

int max(int a, int b) { return a > b ? a : b; }
int min(int a, int b) { return a < b ? a : b; }
int abs(int x) { return x < 0 ? -x : x; }

bool check(int x, int y)
{
    return x > 0 && x <= N && y > 0 && y <= M &&
        !vis[x][y] && G[x][y] != '#' && G[x][y] != '@';
}

int BFS()
{
    if (G[sx][sy] == '@') return -inf;

    Node u, v;
    int i, j;
    u.x = sx;
    u.y = sy;
    u.step = 0;
    queue Q;
    Q.push(u);

    memset(vis, 0, sizeof(vis));

    while (!Q.empty()) {
        u = Q.front(); Q.pop();
        if (u.x == tx && u.y == ty)
            return u.step;
        for (i = 0; i < 8; ++i) {
            v = u;
            v.x += dir[i][0];
            v.y += dir[i][1];
            ++v.step;
            if (abs(u.x - v.x) + abs(u.y - v.y) == 2) {
                int cnt = 0;
                int x1 = min(u.x, v.x);
                int y1 = min(u.y, v.y);
                int x2 = max(u.x, v.x);
                int y2 = max(u.y, v.y);

                if (G[x1][y1] == '#') ++cnt;
                if (G[x1][y2] == '#') ++cnt;
                if (G[x2][y1] == '#') ++cnt;
                if (G[x2][y2] == '#') ++cnt;
                if (cnt >= 2) continue;
            }

            if (check(v.x, v.y)) {
                vis[v.x][v.y] = true;
                Q.push(v);
            }
        }
    }

    return -inf;
}

void solve()
{
    int ret = 0, i;
    for (i = 0; i < vec.size(); ) {
        tx = vec[i++];
        ty = vec[i++];
        G[tx][ty] = '.';
        ret += BFS();
        if (ret < 0) {
            ret = -1;
            break;
        }
        sx = tx;
        sy = ty;
    }
    cout << ret << endl;
}

int main()
{
    int T;
    cin >> T;
    while (T--) {
        cin >> N >> M >> K;
        getMap();
        solve();
    }
    return 0;
}