POJ1189:釘子和小球(DP)
Description
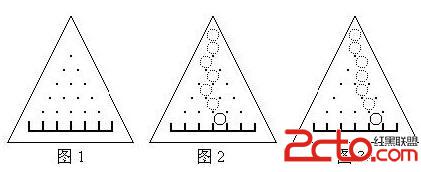
有一個三角形木板,豎直立放,上面釘著n(n+1)/2顆釘子,還有(n+1)個格子(當n=5時如圖1)。每顆釘子和周圍的釘子的距離都等於d,每個格子的寬度也都等於d,且除了最左端和最右端的格子外每個格子都正對著最下面一排釘子的間隙。
讓一個直徑略小於d的小球中心正對著最上面的釘子在板上自由滾落,小球每碰到一個釘子都可能落向左邊或右邊(概率各1/2),且球的中心還會正對著下一顆將要碰上的釘子。例如圖2就是小球一條可能的路徑。
我們知道小球落在第i個格子中的概率pi=pi=
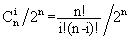
,其中i為格子的編號,從左至右依次為0,1,...,n。
現在的問題是計算拔掉某些釘子後,小球落在編號為m的格子中的概率pm。假定最下面一排釘子不會被拔掉。例如圖3是某些釘子被拔掉後小球一條可能的路徑。
Input
第1行為整數n(2 <= n <= 50)和m(0 <= m <= n)。以下n行依次為木板上從上至下n行釘子的信息,每行中'*'表示釘子還在,'.'表示釘子被拔去,注意在這n行中空格符可能出現在任何位置。
Output
僅一行,是一個既約分數(0寫成0/1),為小球落在編號為m的格子中的概pm。既約分數的定義:A/B是既約分數,當且僅當A、B為正整數且A和B沒有大於1的公因子。
Sample Input
5 2
*
* .
* * *
* . * *
* * * * *
Sample Output
7/16
為了避免小數的計算,我們假設最上面有2^n次方個球,然後求出最後到底層有幾個球,再以這個數字和2^n求GCD得到概率
#include #include #include #include #include #include
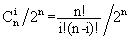 ,其中i為格子的編號,從左至右依次為0,1,...,n。
,其中i為格子的編號,從左至右依次為0,1,...,n。