POJ1178:Camelot(FLOYD+DP)
Description
Centuries ago, King Arthur and the Knights of the Round Table used to meet every year on New Year's Day to celebrate their fellowship. In remembrance of these events, we consider a board game for one player, on which one king and several knight pieces are placed at random on distinct squares.
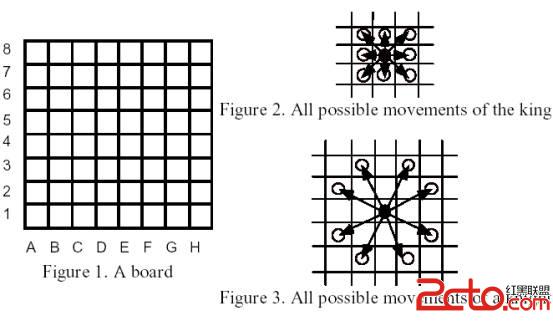
The Board is an 8x8 array of squares. The King can move to any adjacent square, as shown in Figure 2, as long as it does not fall off the board. A Knight can jump as shown in Figure 3, as long as it does not fall off the board.
During the play, the player can place more than one piece in the same square. The board squares are assumed big enough so that a piece is never an obstacle for other piece to move freely.
The player's goal is to move the pieces so as to gather them all in the same square, in the smallest possible number of moves. To achieve this, he must move the pieces as prescribed above. Additionally, whenever the king and one or more knights are placed in the same square, the player may choose to move the king and one of the knights together henceforth, as a single knight, up to the final gathering point. Moving the knight together with the king counts as a single move.
Write a program to compute the minimum number of moves the player must perform to produce the gathering.
Input
Your program is to read from standard input. The input contains the initial board configuration, encoded as a character string. The string contains a sequence of up to 64 distinct board positions, being the first one the position of the king and the remaining ones those of the knights. Each position is a letter-digit pair. The letter indicates the horizontal board coordinate, the digit indicates the vertical board coordinate.
0 <= number of knights <= 63
Output
Your program is to write to standard output. The output must contain a single line with an integer indicating the minimum number of moves the player must perform to produce the gathering.
Sample Input
D4A3A8H1H8
Sample Output
10
題意,有一個國王和n個騎士在一個8*8的棋盤裡,國王可以往鄰近的8個點走,騎士走日字姓,問最後都走到同一個格子需要幾步,要注意國王一旦與一個騎士相遇之後,他們就是一個整體,按騎士的方法來移動
思路:先用floyd求出所有騎士和國王從各個點到其他點的最短路,然後枚舉集合點,枚舉哪位騎士和國王相遇
#include #include #include #include #include #include
