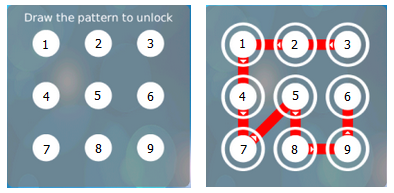
A pattern can be represented using the sequence of points which it's touching for the first time (in the same order of drawing the pattern). And we call those points as active points.For every two consecutive points A and B in the pattern representation, if the line segment connecting A and B passes through some other points, these points must be in the sequence also and comes before A and B, otherwise the pattern will be invalid.In the pattern representation we don't mention the same point more than once, even if the pattern will touch this point again through another valid segment, and each segment in the pattern must be going from a point to another point which the pattern didn't touch before and it might go through some points which already appeared in the pattern.
Now you are given n active points, you need to find the number of valid pattern locks formed from those active points.
Input
There are multiple test cases. The first line of input contains an integer T indicating the number of test cases. For each test case:
The first line contains an integer n (3 ≤ n ≤ 9), indicating the number of active points. The second line contains n distinct integers a1, a2, … an (1 ≤ ai ≤ 9) which denotes the identifier of the active points.
Output
For each test case, print a line containing an integer m, indicating the number of valid pattern lock.
In the next m lines, each contains n integers, indicating an valid pattern lock sequence. The m sequences should be listed in lexicographical order.
Sample Input
1
3
1 2 3
Sample Output
4
1 2 3
2 1 3
2 3 1
3 2 1
手機鎖屏,共9個數,然後給出規定,只能用給定的n個數做密碼,求不同的鎖屏方法有幾種
對於一個點可以走向其他相鄰8個方向,對於中間有相互隔開的情況,例如1到3,如果2已經訪問過,那麼方案是可行的,輸出所有鎖屏方案路徑
#include #include #include #include #include #include