題目如下:
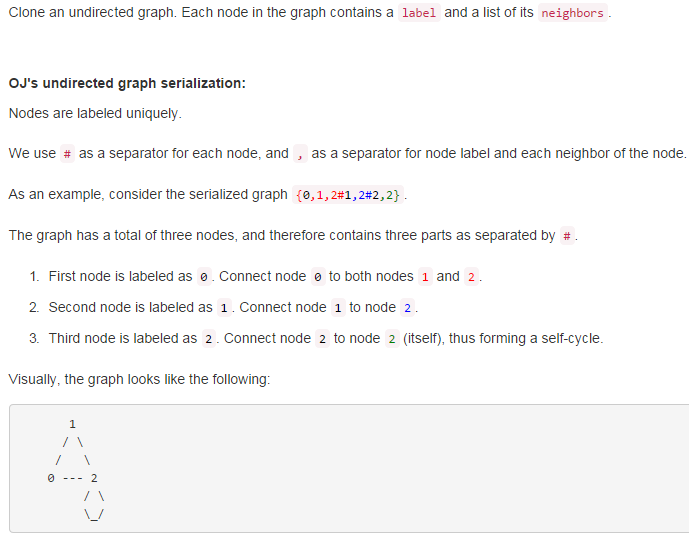
題目挺長的,其實只需要關注第一行就OK了。這道題思路挺明顯的,對於圖來說要麼BFS,要麼DFS,至於具體細節,我覺得與138題:Copy List with Random Pointer很像。在BFS或DFS過程中,可能要調整頂點的鄰接點,這個時候不要忘了它的鄰接點可能還沒有創建。所以,有以下思路:
遍歷兩遍無向圖。第一遍,創建所有結點,不用保存頂點間關系。第二遍,調整頂點間關系。頂點間關系保存在neighbors中,為了能夠找到新創建頂點的位置,第一遍遍歷時候需要保存原頂點與新頂點指針的一一對應關系,這裡可用map或unordered_map保存。
這裡我說的有點啰嗦,請看代碼中注釋就明白了。這裡,我采用BFS遍歷。時間復雜度為O(N),空間復雜度也為O(N)。
1 /**
2 * Definition for undirected graph.
3 * struct UndirectedGraphNode {
4 * int label;
5 * vector<UndirectedGraphNode *> neighbors;
6 * UndirectedGraphNode(int x) : label(x) {};
7 * };
8 */
9 class Solution {
10 public:
11 UndirectedGraphNode* cloneGraph(UndirectedGraphNode *node)
12 {
13 if (node == NULL)
14 {
15 return NULL;
16 }
17
18 map<UndirectedGraphNode*, UndirectedGraphNode*> gphMap;
19 queue<UndirectedGraphNode*> gphQue;
20
21 //創建所有頂點
22 gphQue.push(node);
23 while (!gphQue.empty())
24 {
25 UndirectedGraphNode *tmp = gphQue.front();
26 gphQue.pop();
27
28 if (gphMap.find(tmp) == gphMap.end())
29 {
30 UndirectedGraphNode *newNode = new UndirectedGraphNode(tmp->label);
31 gphMap[tmp] = newNode;
32
33 for (int i = 0; i != tmp->neighbors.size(); ++i)
34 {
35 gphQue.push(tmp->neighbors[i]);
36 }
37 }
38 }
39
40 //調整頂點間關系
41 gphQue.push(node);
42 while (!gphQue.empty())
43 {
44 UndirectedGraphNode *tmp = gphQue.front();
45 gphQue.pop();
46
47 UndirectedGraphNode *exitNode = gphMap[tmp];
48 if (exitNode->neighbors.empty() && !tmp->neighbors.empty())
49 {
50 for (int i = 0; i != tmp->neighbors.size(); ++i)
51 {
52 exitNode->neighbors.push_back(gphMap[tmp->neighbors[i]]);
53 gphQue.push(tmp->neighbors[i]);
54 }
55 }
56 }
57
58 return gphMap[node];
59 }
60 };
其實上面這種方法,是挺清楚直觀的。但還是要考慮一下,能不能優化一下,只遍歷一次。反正,我參加面試時,面試官說:”只遍歷一次,找出(實現)…。其實,實現起來並不難,只需要把兩部分遍歷的操作合並起來就好了。下面我分別給出BFS和DFS算法,兩種算法的時間復雜度都是O(N),空間復雜度也都是O(N)。
實現圖拷貝的BFS算法如下:
1 class Solution {
2 public:
3 UndirectedGraphNode *cloneGraph(const UndirectedGraphNode *node)
4 {
5 if (node == NULL)
6 {
7 return NULL;
8 }
9
10 map<const UndirectedGraphNode*, UndirectedGraphNode*> gphMap;
11 queue<const UndirectedGraphNode *> gphQue;
12
13 gphQue.push(node);
14 gphMap[node] = new UndirectedGraphNode(node->label);
15 while (!gphQue.empty())
16 {
17 const UndirectedGraphNode *tmp = gphQue.front();
18 gphQue.pop();
19
20 for (int i = 0; i != tmp->neighbors.size(); ++i)
21 {
22 if (gphMap.find(tmp->neighbors[i]) == gphMap.end())
23 {
24 //build the vertex
25 UndirectedGraphNode *newNode = new UndirectedGraphNode(tmp->neighbors[i]->label);
26 gphMap[tmp->neighbors[i]] = newNode;
27 gphMap[tmp]->neighbors.push_back(newNode); //Adjust the Vertex
28 gphQue.push(tmp->neighbors[i]);
29 }
30 else
31 {
32 gphMap[tmp]->neighbors.push_back(gphMap[tmp->neighbors[i]]);
33 }
34 }
35 }
36
37 return gphMap[node];
38 }
39 };
實現圖拷貝的DFS算法如下:
1 class Solution {
2 public:
3 UndirectedGraphNode *cloneGraph(const UndirectedGraphNode *node)
4 {
5 if(node == NULL)
6 {
7 return NULL;
8 }
9
10 map<const UndirectedGraphNode*, UndirectedGraphNode*> gphMap;
11
12 return GphClone(node, gphMap); //or return gphMap[node]
13 }
14 private:
15 // DFS
16 static UndirectedGraphNode* GphClone(const UndirectedGraphNode *node,
17 map<const UndirectedGraphNode*, UndirectedGraphNode*> &gphMap)
18 {
19 // a copy already exists
20 if (gphMap.find(node) != gphMap.end())
21 {
22 return gphMap[node];
23 }
24
25 UndirectedGraphNode *newNode = new UndirectedGraphNode(node->label);
26 gphMap[node] = newNode;
27
28 for (int i = 0; i != node->neighbors.size(); ++i)
29 {
30 newNode->neighbors.push_back(GphClone(node->neighbors[i], gphMap));
31 }
32
33 return newNode;
34 }
35 };
雖然時間復雜度都是O(N),但從提交結果看,DFS好像快一點,這個不懂。