Sicily 1422. Table Tennis

Constraints

Time Limit: 1 secs, Memory Limit: 32 MB

Description

There is a rectangular pool table ABCD with side lengths m and n, where m and n are integers with m Assume A,B,C,D is the lower left corner,upper left corner, upper right corner, lower right corner respectively. The length of AB is m, and the length of AD is n.

B---------C
| |
| |
A---------D

Input

Input consist of mutiple cases. Each case include two integers m and n, both of which fits in 32-bit signed integer.

Output

For each case, you should find out which pocket (A,B,C,D) the ball first hit and how many reflections the ball make .

Sample Input

6 10

Sample Output

C 6

假設球撞到邊界時不會反彈，而是繼續進入下一個與原圖一樣大小的邊界，那麼，由於出發的角度是45度，經過了m，n的公倍數的時候就會撞擊一次洞，第一次撞擊自然就是最小公倍數了（這樣的話其實30度60度也是同樣的思路）。見下圖：

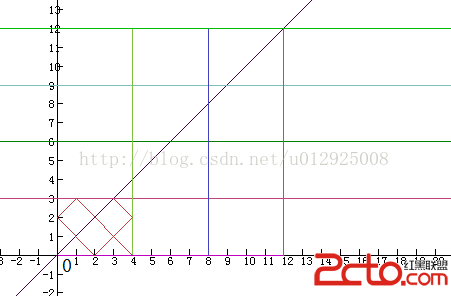
上圖已經顯示得很清晰了，這樣，我們只需計算出最小公倍數，然後計算撞擊橫邊和縱邊的次數，最後再根據撞擊次數確定洞就行：

#include 

int gcd(int a, int b) {//求最大公約數不用遞歸會快
    int c = a % b;
    while (c != 0) {
        a = b;
        b = c;
        c = a % b;
    }
    return b;
}

int main() {
    int n, m, lcm, hit_horizontal_size, hit_vertical_size;
    while (~scanf("%d%d", &m, &n)) {
        lcm = n * m / gcd(n, m);
        hit_horizontal_size = lcm / m - 1;//注意由於最後到洞的時候是不算撞邊的，所以都要減去一
        hit_vertical_size = lcm / n - 1;
        //1 & 1 = 1, 0 & 1 = 0，判斷奇偶這樣快
        if (hit_horizontal_size & 1) {//如果撞擊水平邊的次數是奇數次，那麼可能的點是AD
            if (hit_vertical_size & 1) {//如果撞擊豎直邊的次數是奇數次，那麼可能的點是AB
                printf("A ");
            } else {
                printf("D ");
            }
        } else {
            if (hit_vertical_size & 1) {
                printf("B ");
            } else {
                printf("C ");
            }
        }
        printf("%d\n", hit_horizontal_size + hit_vertical_size);
    }
    return 0;
}