算法簡介:算法的目的是在O(n)的時間復雜度內找到一個字符串中各個字母所在的最大長度的回文串。
此算法用到了一個Rad[]數組的定義,Rad[i]表示回文的半徑,即最大的j滿足s[i-rad[i],i-1]=s[i+1,i+rad[i]]。
很明顯,找到了所有的rad[i],就求出了所有的長度為奇數的回文子串,至於偶數的怎麼求,最後再講.
假設現在求出了rad[1..i-1],現在要求後面的rad值,並且通過前面的操作,得知了當前字符i的rad值至少為j.
現在通過試圖擴大j來掃描,求出了rad[i].再假設現在有個指針k,從1循環到rad[i],試圖通過某些手段來
求出[i+1,i+rad[i]]的rad值.
根據定義,黑色的部分是一個回文子串,兩段紅色的區間全等,因為之前已經求出了rad[i-k],所以直接用它.
有3種情況:
1. rad[i]-k<rad[i-k]
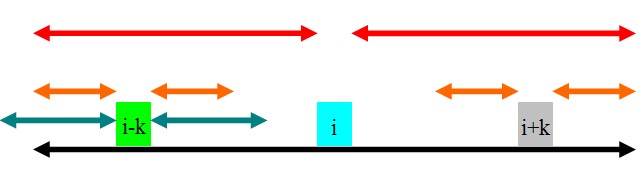
如圖,rad[i-k]的范圍為青色.因為黑色的部分是回文的,且青色的部分超過了黑色的部分,所以rad[i+k]肯定至少為rad[i]-k,
即橙色的部分.那橙色以外的部分就不是了嗎?這是肯定的.因為如果橙色以外的部分也是回文的,那麼根據青色和紅色部分的
關系,可以證明黑色部分再往外延伸一點也是一個回文子串,這肯定不可能,因此rad[i+k]=rad[i]-k.為了方便下文,
這裡的rad[i+k]=rad[i]-k=min(rad[i]-k,rad[i-k]).
2. rad[i]-k>rad[i-k]
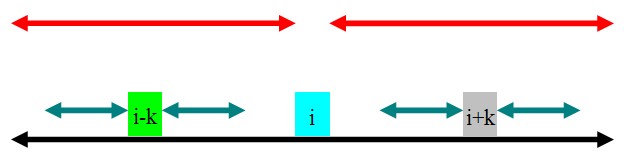
如圖,rad[i-k]的范圍為青色.因為黑色的部分是回文的,且青色的部分在黑色的部分裡面,根據定義,很容易得出:rad[i+k]=rad[i-k].
為了方便下文,這裡的rad[i+k]=rad[i-k]=min(rad[i]-k,rad[i-k]).
根據上面兩種情況,可以得出結論:當rad[i]-k!=rad[i-k]的時候,rad[i+k]=min(rad[i]-k,rad[i-k]).
3. rad[i]-k==rad[i-k]
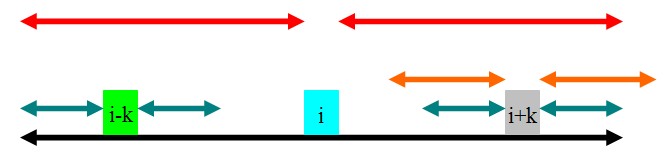
如圖,通過和第一種情況對比之後會發現,因為青色的部分沒有超出黑色的部分,所以即使橙色的部分全等,
也無法像第一種情況一樣引出矛盾,因此橙色的部分是有可能全等的,但是,根據已知的信息,我們不知道橙色的部分是多長,
因此就把i指針移到i+k的位置,j=rad[i-k](因為它的rad值至少為rad[i-k]),等下次循環的時候再做了.
對於長度為偶數的回文子串,一種比較好的方法就是在原來的串中每兩個字符之間加入一個特殊字符,再做.
如:aabbaca,把它變成a#a#b#b#a#c#a,這樣的話,無論原來的回文子串長度是偶數還是奇數,現在都變成奇數了.
1 #include <iostream>
2 #include <string>
3 using namespace std;
4
5 const int maxnum = 1000000;
6
7 int rad[maxnum*2+1];
8
9 int max(int a, int b)
10 {
11 if (a > b) return a;
12 else return b;
13 }
14
15 int min(int a, int b)
16 {
17 if (a < b) return a;
18 else return b;
19 }
20 int manacher(string str)
21 {
22 string s;
23 int n = str.size();
24 int ans = 0;
25 int i, j, k;
26 for (i = 0; i < n; i++)
27 {
28 s += '#';
29 s += str[i];
30 }
31 s += '#';
32
33 n = (n << 1) + 1;
34 i = 0;
35 j = 1;
36 while (i < n)
37 {
38 while (i - j >= 0 && i + j < n && s[i - j] == s[i + j])
39 j++;
40 rad[i] = j - 1;
41 k = 1;
42 while (k <= rad[i] && rad[i] - k != rad[i - k])
43 {
44 rad[i + k] = min(rad[i - k], rad[i] - k);
45 k++;
46 }
47 i += k;
48 j = j - k;
49 }
50 for (i = 0; i < n; i++)
51 ans = max(ans, rad[i]);
52 return ans;
53 }
54
55 int main()
56 {
57 string str;
58 cin >> str;
59 cout << manacher(str) << endl;
60
61 return 0;
62 }