程式師世界 >> 編程語言 >> C語言 >> C++ >> C++入門知識 >> UVA 1331 Minimax Triangulation 區間DP

UVA 1331 Minimax Triangulation 區間DP

編輯：C++入門知識

UVA 1331 Minimax Triangulation 區間DP

區間DP: 將一個多邊形三角剖分,讓可以得到的最大三角形的面積最小

dp[i][j]表示從i點到j點的最優值,枚舉中間點k

dp[i][j]=min(dp[i][j],max(area(i,j,k),max(dp[i][k],dp[k][j])));

注意如果中間三角形i-j-k中有其他的點,這樣的三角形是不可以剖分的

Minimax Triangulation Time Limit: 3000MS Memory Limit: Unknown 64bit IO Format: %lld & %llu

Submit Status

Description

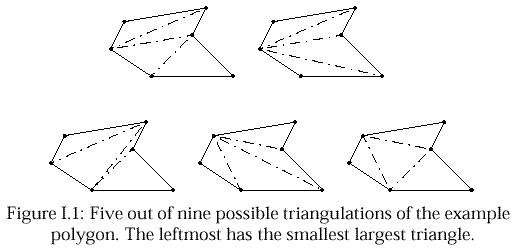
Triangulation of surfaces has applications in the Finite Element Method of solid mechanics. The objective is to estimate the stress and strain on complex objects by partitioning them into small simple objects which are considered incompressible. It is convenient to approximate a plane surface with a simple polygon, i.e., a piecewise-linear, closed curve in the plane on m distinct vertices, which does not intersect itself. A chord is a line segment between two non-adjacent vertices of the polygon which lies entirely inside the polygon, so in particular, the endpoints of the chord are the only points of the chord that touch the boundary of the polygon. A triangulation of the polygon, is any choice of m -3 chords, such that the polygon is divided into triangles. In a triangulation, no two of the chosen chords intersect each other, except at endpoints, and all of the remaining (unchosen) chords cross at least one of the chosen chords. Fortunately, finding an arbitrary triangulation is a fairly easy task, but what if you were asked to find the best triangulation according to some measure?

Input

On the first line of the input is a single pZ喎?http://www.Bkjia.com/kf/ware/vc/" target="_blank" class="keylink">vc2l0aXZlIGludGVnZXIgbiwgdGVsbGluZyB0aGUgbnVtYmVyIG9mIHRlc3Qgc2NlbmFyaW9zIHRvIGZvbGxvdy4gRWFjaCBzY2VuYXJpbyBiZWdpbnMgd2l0aCBhIGxpbmUgY29udGFpbmluZyBvbmUgcG9zaXRpdmUgaW50ZWdlciAyIDwgbSA8IDUwLCBiZWluZyB0aGUgbnVtYmVyIG9mCiB2ZXJ0aWNlcyBvZiB0aGUgc2ltcGxlIHBvbHlnb24uIFRoZSBmb2xsb3dpbmcgbSBsaW5lcyBjb250YWluIHRoZSB2ZXJ0aWNlcyBvZiB0aGUgcG9seWdvbiBpbiB0aGUgb3JkZXIgdGhleSBhcHBlYXIgYWxvbmcgdGhlIGJvcmRlciwgZ29pbmcgZWl0aGVyIGNsb2Nrd2lzZSBvciBjb3VudGVyIGNsb2Nrd2lzZSwgc3RhcnRpbmcgYXQgYW4gYXJiaXRyYXJ5IHZlcnRleC4gRWFjaCB2ZXJ0ZXggaXMgZGVzY3JpYmVkIGJ5IGEgcGFpciBvZiBpbnRlZ2VycwogeCB5IG9iZXlpbmcgMCCh3CB4IKHcIDEwIDAwMCBhbmQgMCCh3CB5IKHcIDEwIDAwMC48L3A+CjxwPjwvcD4KPGgyPk91dHB1dCA8L2gyPgo8cD5Gb3IgZWFjaCBzY2VuYXJpbywgb3V0cHV0IG9uZSBsaW5lIGNvbnRhaW5pbmcgdGhlIGFyZWEgb2YgdGhlIGxhcmdlc3QgdHJpYW5nbGUgaW4gdGhlIHRyaWFuZ3UtbGF0aW9uIG9mIHRoZSBwb2x5Z29uIHdoaWNoIGhhcyB0aGUgc21hbGxlc3QgbGFyZ2VzdCB0cmlhbmdsZS4gVGhlIGFyZWEgc2hvdWxkIGJlIHByZXNlbnRlZCB3aXRoIG9uZSBmcmFjdGlvbmFsIGRlY2ltYWwKIGRpZ2l0LjwvcD4KPHA+PC9wPgo8aDI+U2FtcGxlIElucHV0IDwvaDI+CjxwcmUgY2xhc3M9"brush:java;">1 6 7 0 6 2 9 5 3 5 0 3 1 1

Sample Output

9.0

Source

Root :: AOAPC II: Beginning Algorithm Contests (Second Edition) (Rujia Liu) :: Chapter 9. Dynamic Programming :: Examples
Root :: AOAPC I: Beginning Algorithm Contests -- Training Guide (Rujia Liu) :: Chapter 1. Algorithm Design :: Dynamic Programming :: Exercises: Intermediate

Submit Status

/* ***********************************************
Author        :CKboss
Created Time  :2015年02月12日 星期四 16時24分21秒
File Name     :UVA1331.cpp
************************************************ */

#include 
#include 
#include 
#include 
#include 
#include 
#include 
#include 
#include 
#include 
#include 

using namespace std;

const int maxn=60;
const double INF = 1LL<<30; 
const double eps = 1e-7;

struct Point
{
	double x,y;
	Point(double _x=0,double _y=0):x(_x),y(_y){};
}pt[maxn];

double Area(int a,int b,int c)
{
	Point A=pt[a],B=pt[b],C=pt[c];
	return fabs((B.x-A.x)*(C.y-A.y)-(C.x-A.x)*(B.y-A.y))*0.5;
}

int n;
double dp[maxn][maxn];

double dfs(int l,int r)
{
	if(r==l+1) return dp[l][r]=0;
	if(dp[l][r]>eps) return dp[l][r];

	double temp=INF;
	for(int k=l+1;k