uva 1382 Distant Galaxy （枚舉）

uva 1382 Distant Galaxy

You are observing a distant galaxy using a telescope above the Astronomy Tower, and you think that a rectangle drawn in that galaxy whose edges are parallel to coordinate axes and contain maximum star systems on its edges has a great deal to do with the mysteries of universe. However you do not have the laptop with you, thus you have written the coordinates of all star systems down on a piece of paper and decide to work out the result later. Can you finish this task?

Input

There are multiple test cases in the input file. Each test case starts with one integer N , (1N100) , the number of star systems on the telescope. N lines follow, each line consists of two integers: the X and Y coordinates of the K -th planet system. The absolute value of any coordinate is no more than 10⁹ , and you can assume that the planets are arbitrarily distributed in the universe.

N = 0 indicates the end of input file and should not be processed by your program.

Output

For each test case, output the maximum value you have found on a single line in the format as indicated in the sample output.

Sample Input

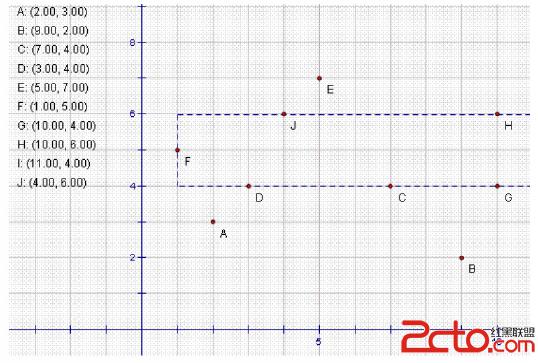
10 
2 3 
9 2 
7 4 
3 4 
5 7 
1 5 
10 4 
10 6 
11 4 
4 6 
0

Sample Output

Case 1: 7

題目大意：給出n個點，問說一個平行與x軸和y軸的矩形，最多能有多少個點落在邊上。

#include
#include
#include
#include
using namespace std;
int n, y[1005], on[1005], on2[1005], L[1005];  
struct point {
	int x, y;
};  
int cmp(point a, point b) {
	return a.x < b.x;
}
point p[1005];
int getAns(){  
	int ans = 0;  
	sort(p, p + n, cmp);  
	sort(y, y + n);  
	int m = unique(y, y + n) - y;  //統計具有不同y坐標的點的個數
	if(m <= 2) return n;  
	for(int a = 0; a < m; a++)          
		for(int b = a + 1; b < m; b++){  
			int miny = y[a], maxy = y[b], k = 0;  //枚舉上下邊
			memset(on, 0, sizeof(on));  
			memset(on2, 0, sizeof(on2));  
			memset(L, 0, sizeof(L));  
			for(int i = 0; i < n; i++){         
				if(!i || p[i].x != p[i-1].x){  
					k++;  
					if(k > 1) L[k] = L[k - 1] + on2[k - 1] - on[k - 1]; //on2記錄邊界,on沒記錄邊界，on2-on就是邊界上的點的個數， 加上上一條豎線左側，就是當前豎線左側點的個數 
				}  
				if(p[i].y < maxy && p[i].y > miny) on[k]++;  
				if(p[i].y <= maxy && p[i].y >= miny) on2[k]++;  
			}  
			if(k <= 2) return n;  
			int Max = 0;  
			for(int i = 1; i <= k; i++){   
				ans = max(ans, L[i] + on2[i] + Max);  //維護Max
				Max = max(Max, on[i] - L[i]);  
			}  
		}  
	return ans;  
}  
int main(){  
	int Case = 1;  
	while(scanf("%d", &n), n){  
		for(int i = 0; i < n; i++){  
			scanf("%d %d", &p[i].x, &p[i].y);  
			y[i] = p[i].y;  
		}  
		printf("Case %d: %d\n", Case++, getAns());  
	}  
	return 0;  
}