poj--2706--Connect(極限大模擬)

poj--2706--Connect(極限大模擬)

Connect Time Limit: 1000MS Memory Limit: 65536K Total Submissions: 1148 Accepted: 375

Description

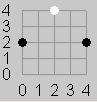
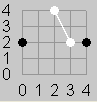
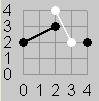
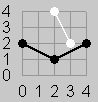
Figure 1 Figure 2 Figure 3a Figure 3b Figure 4
Your task is to decide if a specified sequence of moves in the board game Twixt ends with a winning move.

In this version of the game, different board sizes may be specified. Pegs are placed on a board at integer coordinates in the range [0, N]. Players Black and White use pegs of their own colZ喎?http://www.Bkjia.com/kf/ware/vc/" target="_blank" class="keylink">vci4gQmxhY2sgYWx3YXlzIHN0YXJ0cyBhbmQgdGhlbiBhbHRlcm5hdGVzIHdpdGggV2hpdGUsIHBsYWNpbmcgYSBwZWcKIGF0IG9uZSB1bm9jY3VwaWVkIHBvc2l0aW9uICh4LHkpLiBCbGFjaw=="s endzones are where x equals 0 or N, and White's endzones are where y equals 0 or N. Neither player may place a peg in the other player's endzones. After each play the latest position is connected by a segment to every position with a peg of the same color that is a chess knight's move away (2 away in one coordinate and 1 away in the other), provided that a new segment will touch no segment already added, except at an endpoint. Play stops after a winning move, which is when a player's segments complete a connected path between the player's endzones.

For example Figure 1 shows a board with N=4 after the moves (0,2), (2,4), and (4,2). Figure 2 adds the next move (3,2). Figure 3a shows a poor next move of Black to (2,3). Figure 3b shows an alternate move for Black to (2,1) which would win the game.

Figure 4 shows the board with N=7 after Black wins in 11 moves:
(0, 3), (6, 5), (3, 2), (5, 7), (7, 2), (4, 4), (5, 3), (5, 2), (4, 5), (4, 0), (2, 4).

Input

The input contains from 1 to 20 datasets followed by a line containing only two zeroes, "0 0". The first line of each dataset contains the maximum coordinate N and the number of total moves M where 3 < N < 21, 4 < M < 250, and M is odd. The rest of the dataset contains a total of M coordinate pairs, with one or more pairs per line. All numbers on a line will be separated by a space. M being odd means that Black will always be the last player. All data will be legal. There will never be a winning move before the last move.

Output

The output contains one line for each data set: "yes" if the last move is a winning move and "no" otherwise.

Sample Input

4 5
0 2 2 4 4 2 3 2 2 3
4 5
0 2 2 4 4 2 3 2 2 1
7 11
0 3 6 5 3 2 5 7 7 2 4 4
5 3 5 2 4 5 4 0 2 4
0 0

Sample Output

no
yes
yes

Source

Mid-Central USA 2005

黑白棋的游戲，在n*n的棋盤上，黑棋先手，且最後一步是黑棋。當黑棋從x=0連接的到x=n，時黑棋獲勝，問最後一步是不是致勝的一步

每個點都可以和它周圍的八個點連接，類似象棋中的馬，但是在連接兩個點的時候，在連線之間不能有其他的連線（包括黑棋自身的連線）。所以在連接一條線的時候，要判斷其他的可能會切割這條線的九條線是否存在。

先判斷不包含最後一步的黑棋能不能勝利，再判斷加上最後一步後能不能獲勝，如果開始不能獲勝，後來獲勝，那麼輸出yes，否則，輸出no

#include 
#include 
#include 
#include 
using namespace std ;
int vis[500] ;
int Map[25][25] , c[500][500] ;//ºÚΪ1£¬°×Ϊ-1
queue  que ;
void solve1(int i,int j,int n,int temp)
{
    if( (i-1) >= 0 && (i+1) < n && (j-1) >= 0 && c[ (i-1)*n+j ][ (i+1)*n+(j-1) ] != 0 )
        return ;
    if( (i-1) >= 0 && (j-2) >= 0 && (i+1) < n && (j-1) >= 0 && c[ (i-1)*n+(j-2) ][ (i+1)*n+(j-1) ] != 0 )
        return ;
    if( (j-3) >= 0 && (i+1) < n && (j-1) >= 0 && c[ i*n+(j-3) ][ (i+1)*n+(j-1) ] != 0 )
        return ;
    if( (j-1) >= 0 && (i+1) < n && (j+1) < n && c[ i*n+(j-1) ][ (i+1)*n+(j+1) ] != 0 )
        return ;
    if( (j-1) >= 0 && (i+2) < n && c[ i*n+(j-1) ][ (i+2)*n+j ] != 0 )
        return ;
    if( (j-1) >= 0 && (i+2) < n && (j-2) >= 0 && c[ i*n+(j-1) ][ (i+2)*n+(j-2) ] != 0 )
        return ;
    if( (i-1) >= 0 && (j-1) >= 0 && (i+1) < n && c[ (i-1)*n+(j-1) ][ (i+1)*n+j ] != 0 )
        return ;
    if( (i+1) < n && (j-2) >= 0 && c[ (i+1)*n+j ][ i*n+(j-2) ] != 0 )
        return ;
    if( (j-2) >= 0 && (i+2) < n && (j-1) >= 0 && c[ i*n+(j-2) ][ (i+2)*n+(j-1) ] != 0 )
        return ;
    c[ i*n+j ][ (i+1)*n+(j-2) ] = c[ (i+1)*n+(j-2) ][ i*n+j ] = temp ;
    return ;
}
void solve2(int u,int v,int n,int temp)
{
    if( (u-1) >= 0 && (v-1) >= 0 )
    {
        if( (u+1) < n && c[ (u-1)*n+(v-1) ][ (u+1)*n+v ] != 0 ) return ;
        if( (u+1) < n && (v-2) >= 0 && c[ (u-1)*n+(v-1) ][ (u+1)*n+(v-2) ] != 0 ) return ;
        if( (v-3) >= 0 && c[ (u-1)*n+(v-1) ][ u*n+(v-3) ] != 0 ) return ;
    }
    if( (v-1) >= 0 )
    {
        if( (u-1) >= 0 && (v+1) < n && c[ u*n+(v-1) ][ (u-1)*n+(v+1) ] != 0 ) return ;
        if( (u-2) >= 0 && c[ u*n+(v-1) ][ (u-2)*n+v ] != 0 ) return ;
        if( (u-2) >= 0 && (v-2) >= 0 && c[ u*n+(v-1) ][ (u-2)*n+(v-2) ] != 0 ) return ;
    }
    if( (u+1) < n && (v-1) >= 0 && (u-1) >= 0 && c[ (u+1)*n+(v-1) ][ (u-1)*n+v ] != 0 ) return ;
    if( (u-1) >= 0 && (v-2) >= 0 && c[ (u-1)*n+v ][ u*n+(v-2) ] != 0 ) return ;
    if( (v-2) >= 0 && (u-2) >= 0 && (v-1) >= 0 && c[ u*n+(v-2) ][ (u-2)*n+(v-1) ] != 0 ) return ;
    c[ u*n+v ][ (u-1)*n+(v-2) ] = c[ (u-1)*n+(v-2) ][ u*n+v ] = temp ;
    return ;
}
void solve3(int u,int v,int n,int temp)
{
    if( (u+1) < n )
    {
        if( (u-1) >= 0 && (v-1) >= 0 && c[ (u+1)*n+v ][ (u-1)*n+(v-1) ] != 0 ) return ;
        if( (v-2) >= 0 && c[ (u+1)*n+v ][ u*n+(v-2) ] != 0 ) return ;
        if( (u+2) < n && (v-2) >= 0 && c[ (u+1)*n+v ][ (u+2)*n+(v-2) ] != 0 ) return ;
    }
    if( (u+1) < n && (v-1) >= 0 )
    {
        if( (v+1) < n && c[ (u+1)*n+(v-1) ][ u*n+(v+1) ] != 0 ) return ;
        if( (u+2) < n && (v+1) < n && c[ (u+1)*n+(v-1) ][ (u+2)*n+(v+1) ] != 0 ) return ;
        if( (u+3) < n && c[ (u+1)*n+(v-1) ][ (u+3)*n+v ] != 0 ) return ;
    }
    if( (u+1) < n && (v+1) < n && (v-1) >= 0 && c[ (u+1)*n+(v+1) ][ u*n+(v-1) ] != 0 ) return ;
    if( (v-1) >= 0 && (u+2) < n && c[ u*n+(v-1) ][ (u+2)*n+v ] != 0 ) return ;
    if( (u+2) < n && (u+1) < n && (v-2) >= 0 && c[ (u+2)*n+v ][ (u+1)*n+(v-2) ] != 0 ) return ;
    c[ u*n+v ][ (u+2)*n+(v-1) ] = c[ (u+2)*n+(v-1) ][ u*n+v ] = temp ;
    return ;
}
void solve4(int u,int v,int n,int temp)
{
    if( (u-1) >= 0 )
    {
        if( (u-2) >= 0 && (v-2) >= 0 && c[ (u-1)*n+v ][ (u-2)*n+(v-2) ] != 0 ) return ;
        if( (v-2) >= 0 && c[ (u-1)*n+v ][ u*n+(v-2) ] != 0 ) return ;
        if( (u+1) < n && (v-1) >= 0 && c[ (u-1)*n+v ][ (u+1)*n+(v-1) ] != 0 ) return ;
    }
    if( (u-1) >= 0 && (v-1) >= 0 )
    {
        if( (u-3) >= 0 && c[ (u-1)*n+(v-1) ][ (v-3)*n+v ] != 0 ) return ;
        if( (u-2) >= 0 && (v+1) < n && c[ (u-1)*n+(v-1) ][ (u-2)*n+(v+1) ] != 0 ) return ;
        if( (v+1) < n && c[ (u-1)*n+(v-1) ][ u*n+(v+1) ] != 0 ) return ;
    }
    if( (u-1) >= 0 && (v+1) < n && (v-1) >= 0 && c[ (u-1)*n+(v+1) ][ u*n+(v-1) ] != 0 ) return ;
    if( (v-1) >= 0 && (u-2) >= 0 && c[ u*n+(v-1) ][ (u-2)*n+v ] != 0 ) return ;
    if( (u-2) >= 0 && (v-2) >= 0 && c[ (u-2)*n+v ][ (u-1)*n+(v-2) ] != 0 ) return ;
    c[ u*n+v ][ (u-2)*n+(v-1) ] = c[ (u-2)*n+(v-1) ][ u*n+v ] = temp ;
    return ;
}
int bfs(int u,int n)
{
    int v , i , j ;
    while( !que.empty() ) que.pop() ;
    vis[u] = 1 ;
    que.push(u) ;
    while( !que.empty() )
    {
        u = que.front() ;
        que.pop() ;
        if( u >= (n-1)*n )
            return 1 ;
        for(i = 0 ; i < n*n ; i++)
        {
            if( c[u][i] == 1 && vis[i] == 0 )
            {
                vis[i] = 1 ;
                que.push(i) ;
            }
        }
    }
    return 0 ;
}
void solve(int temp,int n)
{
    int u , v ;
    scanf("%d %d", &u, &v) ;
    Map[u][v] = temp ;
    if( (u+1) < n && (v-2) >= 0 && Map[u][v] == Map[u+1][v-2] )
        solve1(u,v,n,temp);
    if( (u-1) >= 0 && (v+2) < n && Map[u][v] == Map[u-1][v+2] )
        solve1(u-1,v+2,n,temp) ;
    if( (u-1) >= 0 && (v-2) >= 0 && Map[u][v] == Map[u-1][v-2] )
        solve2(u,v,n,temp) ;
    if( (u+1) < n && (v+2) < n && Map[u][v] == Map[u+1][v+2] )
        solve2(u+1,v+2,n,temp) ;
    if( (u+2) < n && (v-1) >= 0 && Map[u][v] == Map[u+2][v-1] )
        solve3(u,v,n,temp) ;
    if( (u-2) >= 0 && (v+1) < n && Map[u][v] == Map[u-2][v+1] )
        solve3(u-2,v+1,n,temp) ;
    if( (u-2) >= 0 && (v-1) >= 0 && Map[u][v] == Map[u-2][v-1] )
        solve4(u,v,n,temp) ;
    if( (u+2) < n && (v+1) < n && Map[u][v] == Map[u+2][v+1] )
        solve4(u+2,v+1,n,temp) ;
}
int main()
{
    int n , m , x , y , u , v , temp , i , j ;
    while( scanf("%d %d", &n, &m) != EOF )
    {
        if( m == 0 && n == 0 ) break ;
        n++ ;
        memset(Map,0,sizeof(vis)) ;
        memset(c,0,sizeof(c)) ;
        temp = 1 ;
        m-- ;
        while( m-- )
        {
            solve(temp,n) ;
            temp = -temp ;
        }
        int k1 = 0 , k2 = 0 ;
        memset(vis,0,sizeof(vis)) ;
        for(j = 0 ; j < n ; j++)
        {
            if(  Map[0][j] == 1 && vis[j] == 0 )
            {
                k1 = bfs(j,n) ;
                if( k1 == 1 ) break ;
            }
        }
        solve(temp,n) ;
        memset(vis,0,sizeof(vis)) ;
        for(j = 0 ; j < n ; j++)
        {
            if(  Map[0][j] == 1 && vis[j] == 0 )
            {
                k2 = bfs(j,n) ;
                if( k2 == 1 ) break ;
            }
        }
        if( k1 == 0 && k2 == 1)
            printf("yes\n") ;
        else
            printf("no\n") ;
    }
    return 0;
}