POJ 3744 Scout YYF I 矩陣快速冪優化--概率dp
點擊打開鏈接
Scout YYF I
Time Limit: 1000MS
Memory Limit: 65536K
Total Submissions: 5416
Accepted: 1491
Description
YYF is a couragous scout. Now he is on a dangerous mission which is to penetrate into the enemy's base. After overcoming a series difficulties, YYF is now at the start of enemy's famous "mine road". This is a very long road, on which there are numbers of mines.
At first, YYF is at step one. For each step after that, YYF will walk one step with a probability of
p, or jump two step with a probality of 1-
p. Here is the task, given the place of each mine, please calculate the probality that YYF can
go through the "mine road" safely.
Input
The input contains many test cases ended with
EOF.
Each test case contains two lines.
The First line of each test case is
N (1 ≤
N ≤ 10) and
p (0.25 ≤
p ≤ 0.75) seperated by a single blank, standing for the number of mines and the probability to walk one step.
The Second line of each test case is N integer standing for the place of N mines. Each integer is in the range of [1, 100000000].
Output
For each test case, output the probabilty in a single line with the precision to 7 digits after the decimal point.
Sample Input
1 0.5
2
2 0.5
2 4
Sample Output
0.5000000
0.2500000
Source
POJ Monthly Contest - 2009.08.23, Simon
有n個雷放在1~100000000的位置上,初始位置是1,走一步的概率是p,走兩步的概率是1-p,求順利通過所有雷的概率。
狀態轉移方程:dp[i]=p*dp[i-1]+(1-p)*dp[i-2],如果直接算會MLE或者TLE,可以轉換成用矩陣快速冪求解。
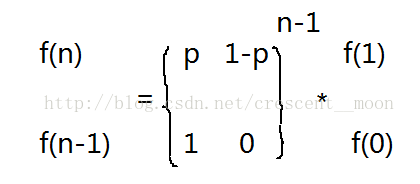
vcDXtcS4xcLKKDEtssi1vcDXtcS4xcLKo6mjrMi7uvPA27PLvs3Kx7TwsLihozwvc3Ryb25nPgo8YnI+Cgo8cHJlIGNsYXNzPQ=="brush:java;">#include
#include
#include
using namespace std;
double p;
int pos[17];
struct Matrax
{
double m[2][2];
}a,per,tmp;
void init()//建立矩陣
{
a.m[0][0]=p;a.m[0][1]=1-p;
a.m[1][0]=1;a.m[1][1]=0;
per.m[0][0]=1;per.m[0][1]=0;
per.m[1][0]=0;per.m[1][1]=1;
}
Matrax multi(Matrax a,Matrax b)//矩陣相乘
{
Matrax c;
for(int i=0;i<2;i++)
for(int j=0;j<2;j++)
{
c.m[i][j]=0;
for(int k=0;k<2;k++)
c.m[i][j]+=a.m[i][k]*b.m[k][j];
}
return c;
}
Matrax power(int k)//矩陣快速冪
{
Matrax pp=a,ans=per;
while(k)
{
if(k&1){ans=multi(ans,pp);k--;}
else {k>>=1;pp=multi(pp,pp);}
}
return ans;
}
int main()
{
int n;
while(scanf("%d%lf",&n,&p)!=EOF)
{
bool no=false;
double ans=1;
memset(pos,0,sizeof(pos));
for(int i=1;i<=n;i++)
scanf("%d",&pos[i]);
sort(pos+1,pos+n+1);
for(int i=1;i<=n;i++)
if(pos[i]==1||pos[i]==pos[i-1]){no=true;break;}
if(no){printf("%.7lf\n",0);continue;}
init();
tmp=power(pos[1]-1);//求從1到第一個雷的概率
ans*=(1-tmp.m[0][0]);//求不到第一個雷的概率
for(int i=2;i<=n;i++)
{
if(pos[i]==pos[i-1])continue;
tmp=power(pos[i]-pos[i-1]-1);//求從第i-1個雷後面一步到第i個雷的概率
ans*=(1-tmp.m[0][0]);//不到第i個雷的概率
}
printf("%.7lf\n",ans);
}
return 0;
}
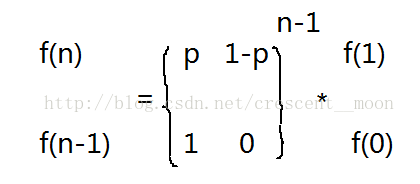 vcDXtcS4xcLKKDEtssi1vcDXtcS4xcLKo6mjrMi7uvPA27PLvs3Kx7TwsLihozwvc3Ryb25nPgo8YnI+Cgo8cHJlIGNsYXNzPQ=="brush:java;">#include
vcDXtcS4xcLKKDEtssi1vcDXtcS4xcLKo6mjrMi7uvPA27PLvs3Kx7TwsLihozwvc3Ryb25nPgo8YnI+Cgo8cHJlIGNsYXNzPQ=="brush:java;">#include