UVA1395 Slim Span（kruskal算法）

UVA1395 Slim Span（kruskal算法）

Slim Span

[PDF Link]

Given an undirected weighted graph G , you should find one of spanning trees specified as follows.

The graph G is an ordered pair (V, E) , where V is a set of vertices {v1, v2,..., vn} and E is a set of undirected edges {e1, e2,..., em} . Each edge e E has its weight w(e) .

A spanning tree T is a tree (a connected subgraph without cycles) which connects all the n vertices with n - 1 edges. The slimness of a spanning tree T is defined as the difference between the largest weight and the smallest weight among the n - 1 edges of T .

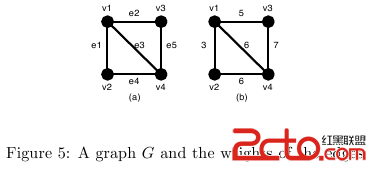
For example, a graph G in Figure 5(a) has four vertices {v1, v2, v3, v4} and five undirected edges {e1, e2, e3, e4, e5} . The weights of the edges are w(e1) = 3 , w(e2) = 5 , w(e3) = 6, w(e4) = 6 , w(e5) = 7 as shown in Figure 5(b).

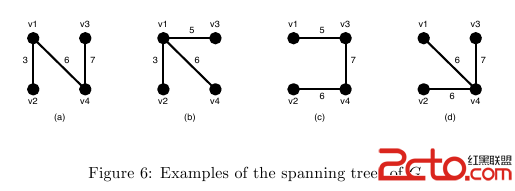
There are several spanning trees for G . Four of them are depicted in Figure 6(a)∼(d). The spanning tree Ta in Figure 6(a) has three edges whose weights are 3, 6 and 7. The largest weight is 7 and the smallest weight is 3 so that the slimness of the tree Ta is 4. The slimnesses of spanning trees Tb , Tc and Td shown in Figure 6(b), (c) and (d) are 3, 2 and 1, respectively. You can easily see the slimness of any other spanning tree is greater than or equal to 1, thus the spanning tree Td in Figure 6(d) is one of the slimmest spanning trees whose slimness is 1.

Your job is to write a program that computes the smallest slimness.

Input

The input consists of multiple datasets, followed by a line containing two zeros separated by a space. Each dataset has the following format.

n m
a1 b1 w1

am bm wm

Every input item in a dataset is a non-negative integer. Items in a line are separated by a space.

n is the number of the vertices and m the number of the edges. You can assume 2n100 and 0mn(n - 1)/2 . ak and bk (k = 1,..., m) are positive integers less than or equal to n , which represent the two vertices vak and vbk connected by the k -th edge ek . wk is a positive integer less than or equal to 10000, which indicates the weight of ek . You can assume that the graph G = (V, E) is simple, that is, there are no self-loops (that connect the same vertex) nor parallel edges (that are two or more edges whose both ends are the same two vertices).

Output

For each dataset, if the graph has spanning trees, the smallest slimness among them should be printed. Otherwise, `-1' should be printed. An output should not contain extra characters.

Sample Input

4 5 
1 2 3
1 3 5
1 4 6
2 4 6
3 4 7
4 6 
1 2 10 
1 3 100 
1 4 90 
2 3 20 
2 4 80 
3 4 40 
2 1 
1 2 1
3 0 
3 1 
1 2 1
3 3 
1 2 2
2 3 5 
1 3 6 
5 10 
1 2 110 
1 3 120 
1 4 130 
1 5 120 
2 3 110 
2 4 120 
2 5 130 
3 4 120 
3 5 110 
4 5 120 
5 10 
1 2 9384 
1 3 887 
1 4 2778 
1 5 6916 
2 3 7794 
2 4 8336 
2 5 5387 
3 4 493 
3 5 6650 
4 5 1422 
5 8 
1 2 1 
2 3 100 
3 4 100 
4 5 100 
1 5 50 
2 5 50 
3 5 50 
4 1 150 
0 0

Sample Output

1 
20 
0 
-1 
-1 
1 
0 
1686 
50

題目大意：

給出一個N結點的圖，求苗條度（最大邊減最小邊的值）盡量最小的生成樹。

解題思路：

首先把邊按權值從小到大排序。對於一個連續的邊集區間【L,R】，如果這些邊使得N個點全部聯通，則一定存在一個苗條度不超過W[R]-W[L]的生成樹。

從小到大枚舉L,對於每個L，從小到大枚舉R，同時用並查集將先進入【L,R】的邊兩端的點合並成一個集合，與kruskal算法一樣。當所有點聯通時停止枚舉R，換下一個L繼續枚舉。