hdu 1568 Fibonacci （數論）

 

Fibonacci

Time Limit: 1000/1000 MS (Java/Others) Memory Limit: 32768/32768 K (Java/Others)
Total Submission(s): 3654 Accepted Submission(s): 1671


Problem Description 2007年到來了。經過2006年一年的修煉，數學神童zouyu終於把0到100000000的Fibonacci數列
(f[0]=0,f[1]=1;f[i] = f[i-1]+f[i-2](i>=2))的值全部給背了下來。
接下來，CodeStar決定要考考他，於是每問他一個數字，他就要把答案說出來，不過有的數字太長了。所以規定超過4位的只要說出前4位就可以了，可是CodeStar自己又記不住。於是他決定編寫一個程序來測驗zouyu說的是否正確。
Input 輸入若干數字n(0 <= n <= 100000000)，每個數字一行。讀到文件尾。
Output 輸出f[n]的前4個數字（若不足4個數字，就全部輸出）。
Sample Input

0
1
2
3
4
5
35
36
37
38
39
40

Sample Output

0
1
1
2
3
5
9227
1493
2415
3908
6324
1023

 

 

 

解析：數論題，智商不夠，就把網上大神的整理的思路簡述一下。

 

用到了斐波那契數列的通項公式。

先看對數的性質,loga(b^c)=c*loga(b),loga(b*c)=loga(b)+loga(c);
假設給出一個數10234432,那麼log10(10234432)=log10(1.0234432*10^7)=log10(1.0234432)+7;

log10(1.0234432)就是log10(10234432)的小數部分.

log10(1.0234432)=0.010063744
10^0.010063744=1.023443198
那麼要取幾位就很明顯了吧~
先取對數(對10取),然後得到結果的小數部分bit,pow(10.0,bit)以後如果答案還是<1000那麼就一直乘10。
注意偶先處理了0~20項是為了方便處理~

這題要利用到數列的公式:an=(1/√5) * [((1+√5)/2)^n-((1-√5)/2)^n](n=1,2,3.....)

取完對數

log10(an)=-0.5*log10(5.0)+((double)n)*log(f)/log(10.0)+log10(1-((1-√5)/(1+√5))^n)其中f=(sqrt(5.0)+1.0)/2.0;
log10(1-((1-√5)/(1+√5))^n)->0
所以可以寫成log10(an)=-0.5*log10(5.0)+((double)n)*log(f)/log(10.0);
最後取其小數部分。

 

 

 

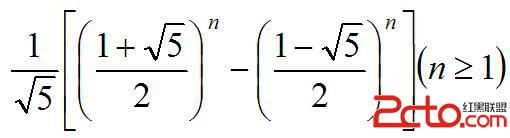
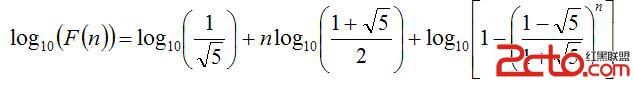
AC代碼：

 

#include
#include
#include
#include
using namespace std;
int f[21] = {0, 1, 1};

int main()
{
//    freopen(in.txt, r, stdin);
	int n;
	for(int i = 2; i < 21; ++i)
		f[i] = f[i - 1] + f[i - 2];
	while(scanf(%d, &n) != EOF)
	{
		if(n <= 20)
		{
			printf(%d
, f[n]);
			continue;
		}
		else
		{
			double temp = -0.5 * log(5.0) / log(10.0) + ((double)n) * log((sqrt(5.0)+1.0)/2.0) / log(10.0);
			temp -= floor(temp);
			temp = pow(10.0, temp);
			while(temp < 1000)
				temp *= 10;
			printf(%d
, (int)temp);
		}
	}
	return 0;
}