User ainta has a permutation p1,?p2,?...,?pn. As the New Year is coming, he wants to make his permutation as pretty as possible.
Permutation a1,?a2,?...,?an is prettier than permutation b1,?b2,?...,?bn, if and only if there exists an integer k (1?≤?k?≤?n) where a1?=?b1,?a2?=?b2,?...,?ak?-?1?=?bk?-?1 and ak?bk all holds.
As known, permutation p is so sensitive that it could be only modified by swapping two distinct elements. But swapping two elements is harder than you think. Given an n?×?n binary matrix A, user ainta can swap the values of pi and pj (1?≤?i,?j?≤?n, i?≠?j) if and only if Ai,?j?=?1.
Given the permutation p and the matrix A, user ainta wants to know the prettiest permutation that he can obtain.
InputThe first line contains an integer n (1?≤?n?≤?300) — the size of the permutation p.
The second line contains n space-separated integers p1,?p2,?...,?pn — the permutation p that user ainta has. Each integer between 1and n occurs exactly once in the given permutation.
Next n lines describe the matrix A. The i-th line contains n characters '0' or '1' and describes the i-th row of A. The j-th character of thei-th line Ai,?j is the element on the intersection of the i-th row and the j-th column of A. It is guaranteed that, for all integers i,?j where 1?≤?i?j?≤?n, Ai,?j?=?Aj,?i holds. Also, for all integers i where 1?≤?i?≤?n, Ai,?i?=?0 holds.
OutputIn the first and only line, print n space-separated integers, describing the prettiest permutation that can be obtained.
Sample test(s) input7 5 2 4 3 6 7 1 0001001 0000000 0000010 1000001 0000000 0010000 1001000output
1 2 4 3 6 7 5input
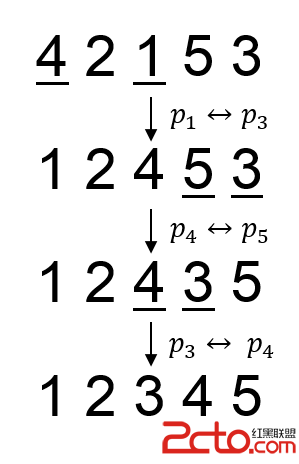
5 4 2 1 5 3 00100 00011 10010 01101 01010output
1 2 3 4 5Note
In the first sample, the swap needed to obtain the prettiest permutation is: (p1,?p7).
In the second sample, the swaps needed to obtain the prettiest permutation is (p1,?p3),?(p4,?p5),?(p3,?p4).
A permutation p is a sequence of integers p1,?p2,?...,?pn, consisting of n distinct positive integers, each of them doesn"t exceed n. Thei-th element of the permutation p is denoted as pi. The size of the permutation p is denoted as n.
題意:給n個數a[],然後給n*n的關系矩陣g[][],如果關系矩陣中a[i][j] == 1,則代表a[i]和a[j]等價,可以交換。問經過交換能得到的字典序最小的序列為多少。
解析:利用Floyd算法,把所有可以直接或間接交換的的關系矩陣都賦值為1,這樣再暴力貪心是能交換的盡可能把小的元素交換到盡可能靠前的位置即可。
AC代碼:
#include#include #include #include #include #include #include #include