1.標題: 世紀末的星期
曾有邪教稱1999年12月31日是世界末日。當然該謠言已經不攻自破。
還有人稱今後的某個世紀末的12月31日,如果是星期一則會....
有趣的是,任何一個世紀末的年份的12月31日都不可能是星期一!!
於是,“謠言制造商”又修改為星期日......
1999年的12月31日是星期五,請問:未來哪一個離我們最近的一個世紀末年(即xx99年)的12月31日正好是星期天(即星期日)?
請回答該年份(只寫這個4位整數,不要寫12月31等多余信息)
2.標題: 振興中華
小明參加了學校的趣味運動會,其中的一個項目是:跳格子。
地上畫著一些格子,每個格子裡寫一個字,如下所示:(也可參見p1.jpg)
從我做起振
我做起振興
做起振興中
起振興中華
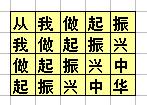
比賽時,先站在左上角的寫著“從”字的格子裡,可以橫向或縱向跳到相鄰的格子裡,但不能跳到對角的格子或其它位置。一直要跳到“華”字結束。
要求跳過的路線剛好構成“從我做起振興中華”這句話。
請你幫助小明算一算他一共有多少種可能的跳躍路線呢?
答案是一個整數,請通過浏覽器直接提交該數字。
注意:不要提交解答過程,或其它輔助說明類的內容。
3.標題: 梅森素數
如果一個數字的所有真因子之和等於自身,則稱它為“完全數”或“完美數”
例如:6 = 1 + 2 + 3
28 = 1 + 2 + 4 + 7 + 14
早在公元前300多年,歐幾裡得就給出了判定完全數的定理:
若 2^n - 1 是素數,則 2^(n-1) * (2^n - 1) 是完全數。
其中 ^ 表示“乘方”運算,乘方的優先級比四則運算高,例如:2^3 = 8, 2 * 2^3 = 16, 2^3-1 = 7
但人們很快發現,當n很大時,判定一個大數是否為素數到今天也依然是個難題。
因為法國數學家梅森的猜想,我們習慣上把形如:2^n - 1 的素數稱為:梅森素數。
截止2013年2月,一共只找到了48個梅森素數。 新近找到的梅森素數太大,以至於難於用一般的編程思路窺其全貌,所以我們把任務的難度降低一點:
1963年,美國伊利諾伊大學為了紀念他們找到的第23個梅森素數 n=11213,在每個寄出的信封上都印上了“2^11213-1 是素數”的字樣。
2^11213 - 1 這個數字已經很大(有3000多位),請你編程求出這個素數的十進制表示的最後100位。
答案是一個長度為100的數字串,請通過浏覽器直接提交該數字。
注意:不要提交解答過程,或其它輔助說明類的內容。
4.標題: 顛倒的價牌
小李的店裡專賣其它店中下架的樣品電視機,可稱為:樣品電視專賣店。
其標價都是4位數字(即千元不等)。
小李為了標價清晰、方便,使用了預制的類似數碼管的標價簽,只要用顏色筆塗數字就可以了(參見p1.jpg)。
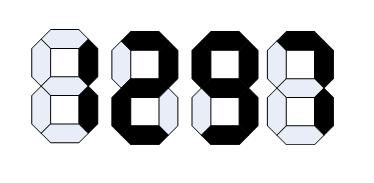
這種價牌有個特點,對一些數字,倒過來看也是合理的數字。如:1 2 5 6 8 9 0 都可以。這樣一來,如果牌子掛倒了,有可能完全變成了另一個價格,比如:1958 倒著掛就是:8561,差了幾千元啊!!
當然,多數情況不能倒讀,比如,1110 就不能倒過來,因為0不能作為開始數字。
有一天,悲劇終於發生了。某個店員不小心把店裡的某兩個價格牌給掛倒了。並且這兩個價格牌的電視機都賣出去了!
慶幸的是價格出入不大,其中一個價牌賠了2百多,另一個價牌卻賺了8百多,綜合起來,反而多賺了558元。
請根據這些信息計算:賠錢的那個價牌正確的價格應該是多少?
答案是一個4位的整數,請通過浏覽器直接提交該數字。
注意:不要提交解答過程,或其它輔助說明類的內容。
5.標題:三部排序
一般的排序有許多經典算法,如快速排序、希爾排序等。
但實際應用時,經常會或多或少有一些特殊的要求。我們沒必要套用那些經典算法,可以根據實際情況建立更好的解法。
比如,對一個整型數組中的數字進行分類排序:
使得負數都靠左端,正數都靠右端,0在中部。注意問題的特點是:負數區域和正數區域內並不要求有序。可以利用這個特點通過1次線性掃描就結束戰斗!!
以下的程序實現了該目標。
static void sort(int[] x)
{
int p = 0;
int left = 0;
int right = x.length-1;
while(p<=right){
if(x[p]<0){
int t = x[left];
x[left] = x[p];
x[p] = t;
left++;
p++;
}
else if(x[p]>0){
int t = x[right];
x[right] = x[p];
x[p] = t;
right--;
}
else{
_________________________; //代碼填空位置
}
}
}
如果給定數組:
25,18,-2,0,16,-5,33,21,0,19,-16,25,-3,0
則排序後為:
-3,-2,-16,-5,0,0,0,21,19,33,25,16,18,25
請分析代碼邏輯,並推測劃線處的代碼,通過網頁提交
注意:僅把缺少的代碼作為答案,千萬不要填寫多余的代碼、符號或說明文字!!
6.標題:逆波蘭表達式
正常的表達式稱為中綴表達式,運算符在中間,主要是給人閱讀的,機器求解並不方便。
例如:3 + 5 * (2 + 6) - 1
而且,常常需要用括號來改變運算次序。
相反,如果使用逆波蘭表達式(前綴表達式)表示,上面的算式則表示為:
- + 3 * 5 + 2 6 1
不再需要括號,機器可以用遞歸的方法很方便地求解。
為了簡便,我們假設:
1. 只有 + - * 三種運算符
2. 每個運算數都是一個小於10的非負整數
下面的程序對一個逆波蘭表示串進行求值。
其返回值為一個數組:其中第一元素表示求值結果,第二個元素表示它已解析的字符數。
static int[] evaluate(String x)
{
if(x.length()==0) return new int[] {0,0};
char c = x.charAt(0);
if(c>='0' && c<='9') return new int[] {c-'0',1};
int[] v1 = evaluate(x.substring(1));
int[] v2 = __________________________________________; //填空位置
int v = Integer.MAX_VALUE;
if(c=='+') v = v1[0] + v2[0];
if(c=='*') v = v1[0] * v2[0];
if(c=='-') v = v1[0] - v2[0];
return new int[] {v,1+v1[1]+v2[1]};
}
請分析代碼邏輯,並推測劃線處的代碼,通過網頁提交。
注意:僅把缺少的代碼作為答案,千萬不要填寫多余的代碼、符號或說明文字!!
7.標題:錯誤票據
某涉密單位下發了某種票據,並要在年終全部收回。
每張票據有唯一的ID號。全年所有票據的ID號是連續的,但ID的開始數碼是隨機選定的。
因為工作人員疏忽,在錄入ID號的時候發生了一處錯誤,造成了某個ID斷號,另外一個ID重號。
你的任務是通過編程,找出斷號的ID和重號的ID。
假設斷號不可能發生在最大和最小號。
要求程序首先輸入一個整數N(N<100)表示後面數據行數。
接著讀入N行數據。
每行數據長度不等,是用空格分開的若干個(不大於100個)正整數(不大於100000)
每個整數代表一個ID號。
要求程序輸出1行,含兩個整數m n,用空格分隔。
其中,m表示斷號ID,n表示重號ID
例如:
用戶輸入:
2
5 6 8 11 9
10 12 9
則程序輸出:
7 9
再例如:
用戶輸入:
6
164 178 108 109 180 155 141 159 104 182 179 118 137 184 115 124 125 129 168 196
172 189 127 107 112 192 103 131 133 169 158
128 102 110 148 139 157 140 195 197
185 152 135 106 123 173 122 136 174 191 145 116 151 143 175 120 161 134 162 190
149 138 142 146 199 126 165 156 153 193 144 166 170 121 171 132 101 194 187 188
113 130 176 154 177 120 117 150 114 183 186 181 100 163 160 167 147 198 111 119
則程序輸出:
105 120
資源約定:
峰值內存消耗(含虛擬機) < 64M
CPU消耗 < 2000ms
請嚴格按要求輸出,不要畫蛇添足地打印類似:“請您輸入...” 的多余內容。
所有代碼放在同一個源文件中,調試通過後,拷貝提交該源碼。
注意:不要使用package語句。不要使用jdk1.6及以上版本的特性。
注意:主類的名字必須是:Main,否則按無效代碼處理。
8.標題:帶分數
100 可以表示為帶分數的形式:100 = 3 + 69258 / 714
還可以表示為:100 = 82 + 3546 / 197
注意特征:帶分數中,數字1~9分別出現且只出現一次(不包含0)。
類似這樣的帶分數,100 有 11 種表示法。
題目要求:
從標准輸入讀入一個正整數N (N<1000*1000)
程序輸出該數字用數碼1~9不重復不遺漏地組成帶分數表示的全部種數。
注意:不要求輸出每個表示,只統計有多少表示法!
例如:
用戶輸入:
100
程序輸出:
11
再例如:
用戶輸入:
105
程序輸出:
6
資源約定:
峰值內存消耗(含虛擬機) < 64M
CPU消耗 < 3000ms
請嚴格按要求輸出,不要畫蛇添足地打印類似:“請您輸入...” 的多余內容。
所有代碼放在同一個源文件中,調試通過後,拷貝提交該源碼。
注意:不要使用package語句。不要使用jdk1.6及以上版本的特性。
注意:主類的名字必須是:Main,否則按無效代碼處理。
9.標題:剪格子
如圖p1.jpg所示,3 x 3 的格子中填寫了一些整數。
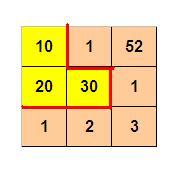
我們沿著圖中的紅色線剪開,得到兩個部分,每個部分的數字和都是60。
本題的要求就是請你編程判定:對給定的m x n 的格子中的整數,是否可以分割為兩個部分,使得這兩個區域的數字和相等。
如果存在多種解答,請輸出包含左上角格子的那個區域包含的格子的最小數目。
如果無法分割,則輸出 0
程序輸入輸出格式要求:
程序先讀入兩個整數 m n 用空格分割 (m,n<10)
表示表格的寬度和高度
接下來是n行,每行m個正整數,用空格分開。每個整數不大於10000
程序輸出:在所有解中,包含左上角的分割區可能包含的最小的格子數目。
例如:
用戶輸入:
3 3
10 1 52
20 30 1
1 2 3
則程序輸出:
3
再例如:
用戶輸入:
4 3
1 1 1 1
1 30 80 2
1 1 1 100
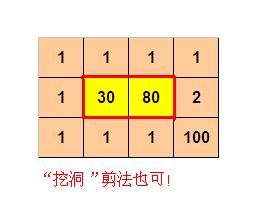
則程序輸出:
10
(參見p2.jpg)
資源約定:
峰值內存消耗(含虛擬機) < 64M
CPU消耗 < 5000ms
請嚴格按要求輸出,不要畫蛇添足地打印類似:“請您輸入...” 的多余內容。
所有代碼放在同一個源文件中,調試通過後,拷貝提交該源碼。
注意:不要使用package語句。不要使用jdk1.6及以上版本的特性。
注意:主類的名字必須是:Main,否則按無效代碼處理。
10.標題:大臣的旅費
很久以前,T王國空前繁榮。為了更好地管理國家,王國修建了大量的快速路,用於連接首都和王國內的各大城市。
為節省經費,T國的大臣們經過思考,制定了一套優秀的修建方案,使得任何一個大城市都能從首都直接或者通過其他大城市間接到達。同時,如果不重復經過大城市,從首都到達每個大城市的方案都是唯一的。
J是T國重要大臣,他巡查於各大城市之間,體察民情。所以,從一個城市馬不停蹄地到另一個城市成了J最常做的事情。他有一個錢袋,用於存放往來城市間的路費。
聰明的J發現,如果不在某個城市停下來修整,在連續行進過程中,他所花的路費與他已走過的距離有關,在走第x千米到第x+1千米這一千米中(x是整數),他花費的路費是x+10這麼多。也就是說走1千米花費11,走2千米要花費23。
J大臣想知道:他從某一個城市出發,中間不休息,到達另一個城市,所有可能花費的路費中最多是多少呢?
輸入格式:
輸入的第一行包含一個整數n,表示包括首都在內的T王國的城市數
城市從1開始依次編號,1號城市為首都。
接下來n-1行,描述T國的高速路(T國的高速路一定是n-1條)
每行三個整數Pi, Qi, Di,表示城市Pi和城市Qi之間有一條高速路,長度為Di千米。
輸出格式:
輸出一個整數,表示大臣J最多花費的路費是多少。
樣例輸入:
5
1 2 2
1 3 1
2 4 5
2 5 4
樣例輸出:
135
樣例說明:
大臣J從城市4到城市5要花費135的路費。
資源約定:
峰值內存消耗(含虛擬機) < 64M
CPU消耗 < 5000ms
請嚴格按要求輸出,不要畫蛇添足地打印類似:“請您輸入...” 的多余內容。
所有代碼放在同一個源文件中,調試通過後,拷貝提交該源碼。
注意:不要使用package語句。不要使用jdk1.6及以上版本的特性。
注意:主類的名字必須是:Main,否則按無效代碼處理。