Dijkstra算法——通過邊實現松弛

Dijkstra算法——通過邊實現松弛

算法思想：每次找到離源點最近的頂點，然後以該頂點為中心進行擴展，最終得到源點到其余所有點的最短路徑.時間復雜度是O(N^2).

基本步驟：

將所有的頂點分為兩部分，已知最短路程的頂點集合S和未知最短路徑的頂點集合V. 最開始，已知最短路徑在集合S中只有源點一個頂點，用book數組來標記哪些點在集合S中.設置源點p到自己的最短路徑為0(即dis[p] = 0). 若存在有源點能直接到達的頂點i，則把dis[i] 設為 e[p][i]. 同時把所有其他(源點不能直接到達的)頂點的最短路徑設為∞.在集合V的所有頂點中選擇一個離源點p最近的頂點u(即dis[u]最小)加入到集合P中. 並考察所有以點u為起點的邊，對每一條邊進行松弛操作.重復第3步，如果集合V為空，則結束，最終得到的dis數組中的值就是源點到所有頂點的最短路徑. 一個點到其余各個頂點的最短路徑也叫做“單源最短路徑”. 這個Dijkstra同樣求最短路徑的圖同樣不能有負權邊，因為擴展到負權邊的時候會產生更短的路徑，有可能破壞了已經更新的點路徑不會改變的性質.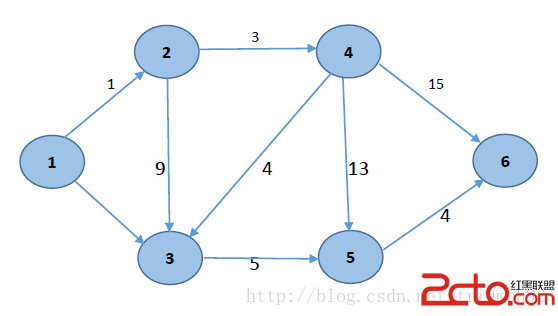

Code:

#include 
#include 
#include 

#define INF 999999
int book[10];          /// 用來紀錄已經是最短路徑的點

int main(int argc, char const *argv[])
{
	int i, j, m, n;
	int q1, q2, q3;
	int u, v, min;
	int e[100][100], dis[10];

	scanf("%d %d", &n, &m);
	for(i = 1; i <= n; ++i)
	{
		for(j = 1; j <= n; ++j)
		{
			if(i == j)
			{
				e[i][j] = 0;
			}
			else
			{
				e[i][j] = INF;
			}
		}
	}

	for(i = 1; i <= m; ++i)
	{
		scanf("%d %d %d", &q1, &q2, &q3);
		e[q1][q2] = q3;
	}

	for(i = 1; i <= n; ++i)
	{
		dis[i] = e[1][i];
	}

	book[1] = 1;              /// Dijkstra 算法核心
	for(i = 1; i < n; ++i)      /// 計算n-1次
	{
		min = INF;
		for(j = 1; j <= n; ++j)
		{
			if(dis[j] < min && book[j] == 0)
			{
				min = dis[j];
				u = j;
			}
		}


		book[u] = 1;
		for(v = 1; v <= n; ++v)
		{
			if(e[u][v] != INF && dis[v] > dis[u] + e[u][v])
			{
				dis[v] = dis[u] + e[u][v];            /// 這個過程就是"松弛"
			}
		}
	}

	for(i = 1; i <= n; ++i)
	{
		printf("%d ", dis[i]);
	}
	printf("\n");

	system("pause");
	return 0;
}