UVA - 10673 - Play with Floor and Ceil （簡單數學！）

題目鏈接：Play with Floor and Ceil

UVA - 10673

Play with Floor and Ceil Time Limit: 3000MS Memory Limit: Unknown 64bit IO Format: %lld & %llu

SubmitStatus

Description

Problem A
Play with Floor and Ceil
Input: standard input
Output: standard output
Time Limit: 1 second

Theorem

For any two integers x and k there exists two more integersp and q such that:

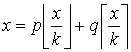
It’s a fairly easy task to prove this theorem, so we’d not ask you to do that. We’d ask for something even easier! Given the values ofx and k, you’d only need to find integers p and q that satisfies the given equation.

Input

The first line of the input contains an integer, T (1≤T≤1000) that gives you the number of test cases. In each of the following T lines you’d be given two positive integersx and k. You can safely assume that x andk will always be less than 10⁸.

Output

For each of the test cases print two integers: p and q in one line. These two integers are to be separated by a single space. If there are multiple pairs ofp and q that satisfy the equation, any one would do. But to help us keep our task simple, please make sure that the values, andfit in a64 bit signed integer.

Sample Input Output for Sample Input

3

5 2

40 2

24444 6

1 1

1 1

0 6

---

Problem setter: Monirul Hasan, Member of Elite Problemsetters' Panel

Special Thanks: Shahriar Manzoor, Member of Elite Problemsetters' Panel

Source

Root :: Prominent Problemsetters :: Monirul Hasan
Root :: Competitive Programming 3: The New Lower Bound of Programming Contests (Steven & Felix Halim) :: Mathematics :: Number Theory ::Extended Euclid
Root :: Competitive Programming 2: This increases the lower bound of Programming Contests. Again (Steven & Felix Halim) :: Mathematics :: Number Theory ::Extended Euclid
Root :: AOAPC I: Beginning Algorithm Contests (Rujia Liu) :: Volume 6. Mathematical Concepts and Methods
Root :: AOAPC I: Beginning Algorithm Contests -- Training Guide (Rujia Liu) :: Chapter 2. Mathematics :: Number Theory ::Exercises: Beginner

數學類簡單題。。

題意：就是找有沒有符合題中那個式子的p和q，有就輸出p和q

思路：先從p入手，0到k掃一邊，如果存在有q可以使式子滿足就break，再輸出p和q

簡單說下floor和ceil，他們都是math頭文件中的庫函數，floor表示向下取整，ceil表示向上取整

在C語言的庫函數中，floor函數的語法如下： #include double floor( double arg ); 功能： 函數返回參數不大於arg的最大整數。例如, x = 6.04; y = floor( x ); y的值為6.0.

ceil則類似。。

AC代碼：

/*************************************************************************
	> File Name: b.cpp
	> Author: zzuspy
	> Mail: [email protected] 
	> Created Time: 2014年12月01日 星期一 21時41分53秒
 ************************************************************************/

#include 
#include 
#include 
#include 
#include 
#include 
#include 
#include 
#define LL long long
#define max3(a,b,c) max(a,max(b,c))
#define min3(a,b,c) min(a,min(b,c))
using namespace std;

int main()
{
	int T;
	scanf("%d", &T);
	while(T--)
	{
		int x, k;
		scanf("%d %d", &x, &k);
		int p, q, fl = (int)floor((double)x/k), ce = (int)ceil((double)x/k);
		for(p = 0; p <= k; p++)
		{
			q = (x-p*fl)/ce;
			if((LL)p*fl+(LL)q*ce == (LL)x)       //判斷q是否成立，這裡p*fl要加個（LL），防止int溢出
				break;
		}
		printf("%d %d\n", p, q);
	}
	return 0;
}