程式師世界 >> 編程語言 >> C語言 >> C++ >> C++入門知識 >> POJ1191——棋盤分割

POJ1191——棋盤分割

編輯：C++入門知識

POJ1191——棋盤分割

棋盤分割 Time Limit: 1000MS Memory Limit: 10000K Total Submissions: 12456 Accepted: 4389

Description

將一個８*８的棋盤進行如下分割：將原棋盤割下一塊矩形棋盤並使剩下部分也是矩形，再將剩下的部分繼續如此分割，這樣割了(n-1)次後，連同最後剩下的矩形棋盤共有n塊矩形棋盤。(每次切割都只能沿著棋盤格子的邊進行)

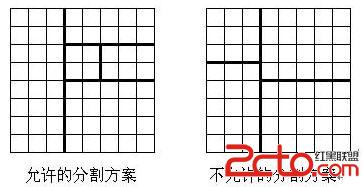
原棋盤上每一格有一個分值，一塊矩形棋盤的總分為其所含各格分值之和。現在需要把棋盤按上述規則分割成n塊矩形棋盤，並使各矩形棋盤總分的均方差最小。
均方差

，其中平均值

，x_i為第i塊矩形棋盤的總分。
請編程對給出的棋盤及n，求出O"的最小值。

Input

第1行為一個整數n(1 < n < 15)。
第2行至第9行每行為8個小於100的非負整數，表示棋盤上相應格子的分值。每行相鄰兩數之間用一個空格分隔。

Output

僅一個數，為O'（四捨五入精確到小數點後三位）。

Sample Input

3
1 1 1 1 1 1 1 3
1 1 1 1 1 1 1 1
1 1 1 1 1 1 1 1
1 1 1 1 1 1 1 1
1 1 1 1 1 1 1 1
1 1 1 1 1 1 1 1
1 1 1 1 1 1 1 0
1 1 1 1 1 1 0 3

Sample Output

1.633

Source

Noi 99

劉汝佳黑書的題，方法書上寫的很詳細，就不贅述了，這應該算是一類二維區間dp吧

#include 
#include 
#include 
#include 
#include 
#include 
#include 
#include 
#include 
#include 
#include 
#include 

using namespace std;

const int inf = 0x3f3f3f3f;
int dp[20][10][10][10][10];
int D[10][10][10][10];
int mat[20][20];
int sum[20][20];

int main()
{
	int n;
	while (~scanf("%d", &n))
		{
			double _x = 0;
			memset (sum, 0, sizeof(sum));
			memset (dp, inf, sizeof(dp));
			for (int i = 1; i <= 8; ++i)
			{
				for (int j = 1; j <= 8; ++j)
				{
					scanf("%d", &mat[i][j]);
				}
				for (int j = 1; j <= 8; ++j)
				{
					sum[i][j] += sum[i][j - 1] + mat[i][j];
				}
			}
			for (int j = 1; j <= 8; ++j)//預處理
			{
				for (int i = 1; i <= 8; ++i)
				{
					sum[i][j] += sum[i - 1][j];
				}
			}
			for (int i = 1; i <= 8; ++i)
			{
				for (int j = 1; j <= 8; ++j)
				{
					for (int k = i; k <= 8; ++k)
					{
						for (int l = j; l <= 8; ++l)
						{
							D[i][j][k][l] = sum[k][l] - sum[k][j - 1] - sum[i - 1][l] + sum[i - 1][j - 1];
							// printf("D[%d][%d][%d][%d] = %d\n", i, j, k, l, D[i][j][k][l]);
							D[i][j][k][l] *= D[i][j][k][l];
						}
					}
				}
			}
			_x = sum[8][8] * 1.0 / n;
			_x *= _x;
			for (int i = 1; i <= 8; ++i)
			{
				for (int j = 1; j <= 8; ++j)
				{
					for (int k = i; k <= 8; ++k)
					{
						for (int l = j; l <= 8; ++l)
						{
							dp[0][i][j][k][l] = D[i][j][k][l];
						}
					}
				}
			}
			for (int i = 1; i < n; ++i)
			{
				for (int j = 1; j <= 8; ++j)/*x1*/
				{
					for (int k = 1; k <= 8; ++k)/*y1*/
					{
						for (int l = j; l <= 8; ++l)/*x2*/
						{
							for (int p = k; p <= 8; ++p)/*y2*/
							{
								for (int q = j; q < l; ++q)
								{
									dp[i][j][k][l][p] = min(min(dp[i][j][k][l][p], dp[i - 1][j][k][q][p] + D[q + 1][k][l][p]), dp[i - 1][q + 1][k][l][p] + D[j][k][q][p]);
								}
								for (int q = k; q < p; ++q)
								{
									dp[i][j][k][l][p] = min(min(dp[i][j][k][l][p], dp[i - 1][j][k][l][q] + D[j][q + 1][l][p]), dp[i - 1][j][q + 1][l][p] + D[j][k][l][q]);
								}
							}
						}
					}
				}
			}
			double t = dp[n - 1][1][1][8][8] * 1.0 / n;
			printf("%.3f\n", sqrt(t - _x));
	}
	return 0;
}