[BZOJ 2875][NOI 2012]隨機數生成器(矩陣快速冪)

[BZOJ 2875][NOI 2012]隨機數生成器(矩陣快速冪)

題目居然沒給描述，我特麼真無語了。。。好吧我來發個題目描述：

給出a,c,g,mod,x0,n,xn=(a*xn-1+c)%mod,求xn%g

聯想用矩陣快速冪在logn的復雜度下求斐波那契數列，對這題我們也可以采取類似的方法。

我們用矩陣運算來改裝這個遞推式：

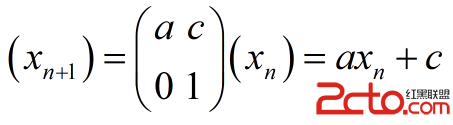
設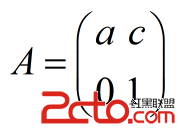

那麼

於是可以直接用矩陣快速冪求A矩陣的n次方，然後再乘上x0即可得出xn

此題還有兩個坑點：

1、xn求出後，先要mod m，再mod g

2、中間運算過程可能爆long long int，所以最好寫個類似於取模快速冪的取模快速乘。

代碼：

#include 
#include 
#include 
#include 
#include 

#define MAXN 3

using namespace std;

typedef unsigned long long int LL;

LL mod,a,c,x0,n,g;

struct matrix
{
    int n,m;
    LL p[MAXN][MAXN];
};

LL fastmul(LL x,LL y) //快速乘x*y
{
    LL ans=0;
    while(y)
    {
        if(y&1) ans+=x,ans=(ans>mod?ans-mod:ans);
        x+=x;
        x=(x>mod?x-mod:x);
        y>>=1;
    }
    return ans;
}

matrix operator*(matrix a,matrix b)
{
    matrix c;
    c.n=a.n;
    c.m=b.m;
    for(int i=1;i<=a.n;i++)
        for(int j=1;j<=b.m;j++)
        {
            c.p[i][j]=0;
            for(int k=1;k<=a.m;k++)
                c.p[i][j]=(c.p[i][j]+(fastmul(a.p[i][k],b.p[k][j]))%mod)%mod;
        }
    return c;
}

matrix fastPow(matrix base,LL pow)
{
    matrix tmp=base,ans;
    memset(ans.p,0,sizeof(ans.p));
    for(int i=1;i<=2;i++)
        ans.p[i][i]=1;
    ans.n=ans.m=2;
    while(pow>0)
    {
        if(pow&1)
            ans=ans*tmp;
        tmp=tmp*tmp;
        pow>>=1;
    }
    return ans;
}

int main()
{
    scanf(%llu%llu%llu%llu%llu%llu,&mod,&a,&c,&x0,&n,&g);
    matrix x,y;
    x.n=x.m=y.n=y.m=2;
    x.p[1][1]=a%mod;
    x.p[1][2]=0;
    x.p[2][1]=c%mod;
    x.p[2][2]=1;
    matrix ans=fastPow(x,n);
    LL xn=fastmul(ans.p[1][1],x0)+ans.p[2][1];
    printf(%llu
,(xn%mod)%g);
    return 0;
}