程式師世界 >> 編程語言 >> C語言 >> C++ >> C++入門知識 >> 分形幾何算法和實現(C語言)，分形幾何算法c語言

分形幾何算法和實現(C語言)，分形幾何算法c語言

編輯：C++入門知識

分形幾何算法和實現(C語言)，分形幾何算法c語言

初識分形

1、分形的含義：

英文單詞Fractal，它是由美籍法國數學家曼德勃羅（Benoit Mandelbrot）創造出來的。其含義是不規則的、破碎的、分數的。曼德勃羅是想用此詞來描述自然界中傳統歐幾裡得幾何學所不能描述的一大類復雜無規的幾何對象。

2、分形的幾何特征：

自相似性：自相似，便是局部與整體的相似。

自仿射性：自仿射性是自相似性的一種拓展。如果，將自相似性看成是局部到整體在各個方向上的等比例變換的結果的話，那麼，自仿射性就是局部到整體在不同方向上的不等比例變換的結果。前者稱為自相似變換，後者稱為自仿射變換。

精細結構：任意小局部總是包含細致的結構。

3、分形與計算機科學：

分形理論的發展離不開計算機圖形學的支持，如果一個分形構造的表達，不用計算機的幫助是很難讓人理解的。不僅如此，分形算法與現有計算機圖形學的其他算法相結合，還會產生出非常美麗的圖形，而且可以構造出復雜紋理和復雜形狀，從而產生非常逼真的物質形態和視覺效果。

分形作為一種方法，在圖形學領域主要是利用迭代、遞歸等技術來實現某一具體的分形構造。

分形幾何學與計算機圖形學相結合，將會產生一門新的學科——分形圖形學。它的主要任務是以分形幾何學為數學基礎，構造非規則的幾何圖素，從而實現分形體的可視化，以及對自然景物的逼真模擬。

本文地址：http://www.cnblogs.com/archimedes/p/fractal-c.html，轉載請注明源地址。

分形圖的遞歸算法

遞歸算法就不贅述了，凡是搞編程的應該都不陌生，可以參考我早前寫過的一些遞歸程序題目小練一下:《遞歸練習(C語言)》

以Koch曲線的遞歸算法為例：

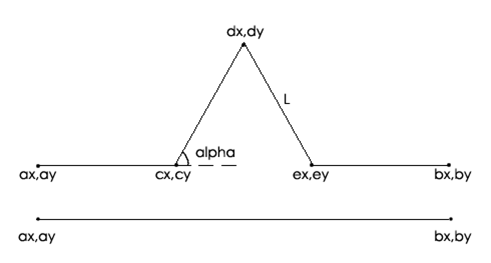
代碼如下：

#include<stdio.h>
#include<math.h>
#include<conio.h>
#include"graphics.h"
void  koch(double x0, double y0, double x1, double y1, int k)
{
    double x2, y2, x3, y3, x4, y4;
    x2 = 2.0/3 * x0 + 1.0/3 * x1;  /*由上面的運算可以得到其余三點 坐標的計算式*/
    y2 = 2.0/3 * y0 + 1.0/3 * y1;
    x3 = 1.0/3 * x0 + 2.0/3 * x1;
    y3 = 1.0/3 * y0 + 2.0/3 * y1;
    x4 = 1.0/2 * (x0 + x1) - sqrt(3.0)/6 * (y1 - y0);
    y4 = 1.0/2 * (y0 + y1) + sqrt(3.0)/6 * (x1 - x0);
    if( k > 1)    /*如果迭代次數大於1，就繼續迭代下去，即執行以下程序*/
    {
        koch(x0, y0, x2, y2, k - 1);  /*對以(x0, y0)和(x2, y2)為端點的線段作為
        初始線段進行迭代運算，以下類同*/
        koch(x2, y2, x4, y4, k - 1);
        koch(x4, y4, x3, y3, k - 1);
        koch(x3, y3, x1, y1, k - 1);
    } else {      /*如果迭代次數等於1，停止迭代，畫出迭代生成的圖形*/
        line(x0, y0, x2, y2);       /*用直線聯結兩點(x0, y0)和(x2, y2)*/
        line(x2, y2, x4, y4);       /*用直線聯結兩點(x2, y2)和(x4, y4)*/
        line(x4, y4, x3, y3);       /*用直線聯結兩點(x4, y4)和(x3, y3)*/
        line(x3, y3, x1, y1);       /*用直線聯結兩點(x3, y3)和(x1, y1)*/
    }
}

int main()
{
    int n, gdriver = DETECT, gmode;      /*定義迭代次數n*/
    initgraph(&gdriver, &gmode,"C:\\Win-TC\\BGI");     /*圖形系統初始化*/
    printf("Please input the value of the positive integer n (n<9):");
    scanf("%d", &n);               /*輸入迭代次數n*/
    setcolor(GREEN);
    koch(50, 120, 450, 120, n);
    getch();
    closegraph(); /*關閉圖形系統*/
    return 0;
}

LS文法

LS文法先定義了繪圖規則：

F：以當前方向前進一步，並畫線；

f：以當前方向前進一步，不畫線；

＋：逆時針旋轉角；

－：順時針旋轉角；

[：表示暫時保存當前的畫圖狀態；

]：表示提取出保存的畫圖狀態。 “[”和“]”要成對的出現。

Koch曲線的LS文法如下：

w：F（初始字母）

a ：60(旋轉角度)

P：F → F ＋ F －－ F ＋ F（F的替代文法）

根據這一文法生成Koch曲線的步驟（假設迭代兩次）：

第一步：得到迭代兩次的文法。

第一次迭代結果：

F ＋ F －－ F ＋ F

第二次迭代結果：(第一次迭代得到的結果的每一個F用規則P替換)

F ＋ F －－ F ＋ F ＋ F ＋ F －－ F ＋ F －－ F ＋ F －－ F ＋ F ＋ F ＋ F －－ F ＋ F

第二步：按照迭代得到的文法繪圖。

當然，還有實現其他分形圖的LS文法，這裡就不一一舉出了

下面的算法沒有用遞歸，純C語言實現：

/****************************************************
** Completed on 2014.11.11 11:11
** Programming environment：win xp + win-tc 2.0
** Language: ANSI C
** copyright(c)  codingwu   (Email: [email protected])
*****************************************************/
#include<stdio.h>
#include<stdlib.h>
#include<math.h>
#include<string.h>
#include<ctype.h>
#include<malloc.h>
#include<conio.h>
#include<graphics.h>

#define PI 3.1415926
#define stacksize 1024

typedef struct _point {
    double x;
    double y;
    double delta;
}point;

typedef struct _L_Sys {
    char *name;
    char *startStr; /* 初始字符串 */
    char *replaceF;
    char *replaceX;  /* 替換X字符串 */
    char *replaceY;  /* 替換Y字符串 */
    char *replaceS;  /* 替換S字符串 */
    char *replaceG;  /* 替換G字符串 */
    char *replaceK;  /* 替換K字符串 */
    char *replaceL;  /* 替換L字符串 */
    char *replaceH;  /* 替換H字符串 */
    int StartX;  /* 起始點坐標 */
    int StartY;
    int depth;   /* 遞歸深度 */
    int ruleNumber;  /* 規則數 */
    double angle;
    double direct_init;
    double length;

}L_Sys;

L_Sys ls[100];

void init_L_Sys(L_Sys *LS, char *_name, char *_startStr, char *_replaceF,
        char *_replaceX, char *_replaceY, char *_replaceS, char *_replaceG,
        char *_replaceK, char *_replaceL, char *_replaceH,  int _StartX,
        int _StartY, int _depth, int _ruleNumber, double _angle,
        double _direct_init, double _length)    /* 初始化 */
{
    (*LS).name = (char *)malloc(strlen(_name) + 1);
    if((*LS).name == NULL) return;
    strcpy((*LS).name, _name);
    (*LS).startStr = (char *)malloc(strlen(_startStr) + 1);
    if((*LS).startStr == NULL) return;
    strcpy((*LS).startStr, _startStr);
    (*LS).replaceF = (char *)malloc(strlen(_replaceF) + 1);
    if((*LS).replaceF == NULL) return;
    strcpy((*LS).replaceF, _replaceF);
    (*LS).replaceX = (char *)malloc(strlen(_replaceX) + 1);
    if((*LS).replaceX == NULL) return;
    strcpy((*LS).replaceX, _replaceX);
    (*LS).replaceY = (char *)malloc(strlen(_replaceY) + 1);
    if((*LS).replaceY == NULL) return;
    strcpy((*LS).replaceY, _replaceY);
    (*LS).replaceS = (char *)malloc(strlen(_replaceS) + 1);
    if((*LS).replaceS == NULL) return;
    strcpy((*LS).replaceS, _replaceS);
    (*LS).replaceG = (char *)malloc(strlen(_replaceG) + 1);
    if((*LS).replaceG == NULL) return;
    strcpy((*LS).replaceG, _replaceG);
    (*LS).replaceK = (char *)malloc(strlen(_replaceK) + 1);
    if((*LS).replaceK == NULL) return;
    strcpy((*LS).replaceK, _replaceK);
    (*LS).replaceL = (char *)malloc(strlen(_replaceL) + 1);
    if((*LS).replaceL == NULL) return;
    strcpy((*LS).replaceL, _replaceL);
    (*LS).replaceH = (char *)malloc(strlen(_replaceH) + 1);
    if((*LS).replaceH == NULL) return;
    strcpy((*LS).replaceH, _replaceH);
    (*LS).StartX = _StartX;
    (*LS).StartY = _StartY;
    (*LS).depth = _depth;
    (*LS).ruleNumber = _ruleNumber;
    (*LS).angle = _angle;
    (*LS).direct_init = _direct_init;
    (*LS).length = _length;
}

void init(int n)
{
 /*init_L_Sys(&ls[i], "hualei", "Start", "F", "X", "Y", "S", "G", "K", "L", "H",
        pStartX, pStartY, depth, ruleNumber, angle, direct_init, length);          */
    switch(n) {
    case 0:
        init_L_Sys(&ls[0], "xiecao", "G", "F-XF", "", "", "",
            "GFX[+++++GFG][-----GFG]", "", "", "", 340, 20, 6, 2, -3, 60, 3.3);
        break;
    case 1:
        init_L_Sys(&ls[1], "shusan", "X", "FF", "--FXF++FXF++FXF--", "", "",
            "", "", "", "", 200, 50, 6, 2, -60, 0, 6);
        break;
    case 2:
        init_L_Sys(&ls[2], "hualei", "F", "F[+F[+F][-F]F][-F[+F][-F]F]F[+F][-F]F",
         "", "", "", "", "", "", "", 200, 20, 5, 1, 30, 90, 6);
        break;
    case 3:
        init_L_Sys(&ls[3], "shuzhi", "K", "", "", "", "[+++G][---H]FFS",
        "G+G[-FH]F", "FSF", "", "-H[+FG]F",
        200, 210, 13, 4, -18, -90, 9.5);
        break;
    case 4:
        init_L_Sys(&ls[4], "shuzhi", "F", "F[+F]F[-F]F", "", "", "",
        "", "", "", "",
        200, 5, 6, 1, -25.7341, 90, 1.5);
        break;
    case 5:
        init_L_Sys(&ls[5], "korch", "F", "F[+F]F[-F]F", "", "", "",
        "", "", "", "",
        200, 5, 6, 1, -25.7341, 90, 1.5);
        break;    
    case 6:
        init_L_Sys(&ls[6], "pugongying", "Y", "", "X[-FFF][+FFF]FX",
        "YFX[+Y][-Y]", "", "", "", "", "",
        200, 10, 10, 2, 30, 90, 0.37);
        break;    
    case 7:
        init_L_Sys(&ls[7], "guanmucong", "F", "FF-[-F+F+F]+[+F-F-F]", "", "",
         "", "", "", "", "",
        250, 20, 6, 1, -30, 90, 3.5);
        break;    

    case 8:
        init_L_Sys(&ls[8], "kaihuadecao", "G", "", "XFX", "", "",
        "[+FGF][-FGF]XG", "", "", "",
        200, 10, 8, 2, -30, 90, 3);
        break;
    case 9:
        init_L_Sys(&ls[9], "guanmucong2", "F",
        "F[+++++++++++++++++++++++++F]-F[-------------------------F]F", "", "",
        "", "", "", "", "",
        370, 30, 6, 1, -1.2, 90, 2);
        break;
    case 10:
        init_L_Sys(&ls[10], "yangliu", "F", "FF+[+F-F-F]-[-F+F+F]", "", "",
        "", "", "", "", "", 170, 0, 5, 1, -22.5, 90, 7);
        break;
    case 11:
        init_L_Sys(&ls[11], "Juliet", "X", "", "X+YF+", "-FX-Y", "", "", "", "", "",
        95, 250, 17, 2, 90, 0, 1);
    case 12:
        init_L_Sys(&ls[12], "zhuanqiang", "X", "", "XFYFX+F+YFXFY-F-XFYF",
         "YFXFY-F-XFYFX+F+YFXFY", "", "", "", "", "",
        30, 40, 4, 2, 90, 0, 13);
        break;
    case 13:
        init_L_Sys(&ls[13], "zhuanqiang_X", "F+F+F+F", "F+F-F-FF+F+F-F", "",
         "", "", "", "", "", "",
        80, 90, 4, 1, 90, 0, 3.5);
        break;
    case 14:
        init_L_Sys(&ls[14], "sanjiaoraosanjiao", "X", "FFF", "--FXF++FXF++FXF--",
         "", "", "", "", "", "",
        200, 10, 6, 2, -60, 0, 1.7);
        break;
    case 15:
        init_L_Sys(&ls[15], "yibimigong", "X", "", "-YF+XFX+FY-", "+XF-YFY-FX+",
         "", "", "", "", "",
        50, 30, 6, 2, -90, 0, 10);
    case 16:
        init_L_Sys(&ls[16], "shu", "X", "FF", "F[+X]F[-X]+X", "", "", "", "", "", "",
        200, 10, 10, 2, 30, 90, 0.35);
    case 17:
        init_L_Sys(&ls[17], "duichengdeshu", "X", "FF", "F[+X][-X]FX", "", "",
        "", "", "", "",
        200, 10, 10, 2, 30, 90, 0.35);
        break;
    default:
        break;
    }
    return;

}

void freeMemory(L_Sys *LS)  /* 釋放內存 */
{
    free((*LS).name);
    (*LS).name = NULL;
    free((*LS).startStr);
    (*LS).startStr = NULL;
    free((*LS).replaceF);
    (*LS).replaceF = NULL;
    free((*LS).replaceX);
    (*LS).replaceX = NULL;
    free((*LS).replaceY);
    (*LS).replaceY = NULL;
    free((*LS).replaceS);
    (*LS).replaceS = NULL;
    free((*LS).replaceG);
    (*LS).replaceG = NULL;
    free((*LS).replaceK);
    (*LS).replaceK = NULL;
    free((*LS).replaceL);
    (*LS).replaceL = NULL;
    free((*LS).replaceH);
    (*LS).replaceH = NULL;
}

void fileCopy(FILE *dest, FILE *src) /* 復制文件函數 */
{
    char ch;
    fseek(src, 0, SEEK_SET);
    ch = fgetc(src);
    while(ch != EOF) {
        fputc(ch, dest);
        ch = fgetc(src);
    }
}

void fractal(int curr_string)  /* 核心功能函數 */
{
    int i, j, k, size, depth, len;
    char a[2], ch;
    double Delta;
    FILE *result, *tmp;
    point stack[stacksize];
    point *p;
    point bef, aft;

    tmp = fopen("B.txt","w+");
    if(tmp == NULL) return;
    init(curr_string);
    p = stack;
    fputs(ls[curr_string].startStr, tmp);
    depth = ls[curr_string].depth;
    len =  ls[curr_string].length;
    for(i = 0; i < depth; i++) {
        result = fopen("A.txt","w+");
        if(result == NULL) return;

        fseek(tmp, 0, SEEK_SET);
        ch = fgetc(tmp);
        while(ch != EOF) {      /* F X Y S G K L H*/
            if(ch == 'F') {
                fputs(ls[curr_string].replaceF, result);
            } else if (ch == 'X') {
                fputs(ls[curr_string].replaceX, result);
            } else if (ch == 'Y') {
                fputs(ls[curr_string].replaceY, result);
            } else if (ch == 'S') {
                fputs(ls[curr_string].replaceS, result);
            } else if (ch == 'G') {
                fputs(ls[curr_string].replaceG, result);
            } else if (ch == 'K') {
                fputs(ls[curr_string].replaceK, result);
            } else if (ch == 'L') {
                fputs(ls[curr_string].replaceL, result);
            } else if (ch == 'H') {
                fputs(ls[curr_string].replaceH, result);
            } else {
                fputc(ch, result);
            }
            ch = fgetc(tmp);
        }
       fseek(tmp, 0, SEEK_SET);
       fileCopy(tmp, result);
       fclose(result);
    }
    bef.x = ls[curr_string].StartX;
    bef.y = ls[curr_string].StartY;

    bef.delta = PI * (ls[curr_string].angle)/180;
    Delta = PI * (ls[curr_string].angle)/180;   /* 轉換為弧度制 */

    result = fopen("A.txt","r");
    fseek(result, 0, SEEK_SET);
    ch = fgetc(result);
    while(ch != EOF) {

        switch(ch) {
        case 'F':
        case 'X':
        case 'Y':
        case 'S':
        case 'G':
        case 'K':
        case 'L':
        case 'H':
            aft.x = bef.x + len * cos(bef.delta);
            aft.y = bef.y - len * sin(bef.delta);
            aft.delta = bef.delta;
            line(bef.x, 400 - bef.y, aft.x, 400 - aft.y);

            bef.x = aft.x;
            bef.y = aft.y;
            bef.delta = aft.delta;
            break;
        case '+':
            bef.delta += Delta;
            break;
        case '-':
            bef.delta -= Delta;
            break;
        case '[':
            *(p++) = bef;
            break;
        case ']':
            bef = *(--p);
            break;
        default:
            break;
        }
        ch = fgetc(result);
    }
    fclose(tmp);
    fclose(result);
    freeMemory(&ls[curr_string]);
}

int main(void)
{
    char ch;
    int n, gdriver = DETECT, gmode;
    wu:
    printf("xiecao:0  shusan:1  hualei:2  shuzhi1:3  shuzhi2:4\n");   /* 說明 */
    printf("korch:5  pugongying:6  guanmucong:7  kaihuadecao:8  guanmucong2:9\n");
    printf("yangliu:10  Juliet:11  zhuanqiang:12  zhuanqiang_X:13  sanjiaoraosanjiao:14\n");
    printf("yibimigong:15  shu:16  duichengdeshu:17\n");
    printf("guanmucong2:9\n");
    printf("continue?(Y/N)\n");
    ch = getchar();
    if(ch == 'n' || ch == 'N')
        return 0;
    else {
        printf("please input a non-negative number to choose which image you what to see(0 <= n <= 17 ): ");
        scanf("%d", &n);

        initgraph(&gdriver, &gmode,"C:\\Win-TC\\BGI");  /*圖形系統初始化*/
        setcolor(GREEN);  /* 設置畫筆的顏色 */
        fractal(n);
        getch();
        closegraph();  /*關閉圖形系統*/
        getchar();
        goto wu;
    }
    return 0;
}