zzu--2014年11月16日月賽 B題

zzu--2014年11月16日月賽 B題

Description

Mad scientist Mike is building a time machine in his spare time. To finish the work, he needs a resistor with a certain resistance value.

However, all Mike has is lots of identical resistors with unit resistance R0?=?1. Elements with other resistance can be constructed from these resistors. In this problem, we will consider the following as elements:

1. one resistor;
2. an element and one resistor plugged in sequence;
3. an element and one resistor plugged in parallel.

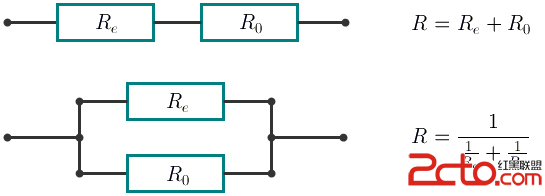
   With the consecutive connection the resistance of the new element equals R = Re + R0. With the parallel connection the resistance of the new element equals . In this case Reequals the resistance of the element being connected.

   Mike needs to assemble an element with a resistance equal to the fraction . Determine the smallest possible number of resistors he needs to make such an element.

   Input

   The single input line contains two space-separated integers a and b (1 <= a, b <= 1^18). It is guaranteed that the fraction is irreducible. It is guaranteed that a solution always exists.

   Output

   Print a single number — the answer to the problem.

   Please do not use the %I64d specifier to read or write 64-bit integers in С++. It is recommended to use the cin, cout streams or the%lld specifier.

   Sample Input

   1 13 2199 200

   Sample Output

   13200

   HINT

   In the first sample, one resistor is enough.

   
   

   In the second sample one can connect the resistors in parallel, take the resulting element and connect it to a third resistor consecutively. Then, we get an element with resistance . We cannot make this element using two resistors.

   Source

   CF

   
   

   
   

   題意：就是去找最少要多少個電阻可以達成功能！

   
   

   思路：如果 a/b > 1 則 a/b 整數部分可以加到ans，a再模b； 如果a == b 則ans += a ， a變為0； 如果 a/b < 1 則b/a 整數部分可以加到ans，b再模a

   
   

   例如：3/5 要先變為1 / ( 2 / 3 +1 ) ，ans=1，然後變為 1 / ( 1 / 2 + 1 ) ， ans=2，最後1 /（1 + 1），ans =4

   
   

   AC代碼：

   #include 
   #include 
   #include 
   #define ll long long
   using namespace std;
   
   int main()
   {
   	ll a, b;
   	while(scanf("%lld %lld", &a, &b)!=EOF)
   	{
   		ll ans = 0;
   		while(a)
   		{
   			if(a > b)
   			{
   				ll t = a / b;
   				ans+=t;
   				a=a%b;
   			}
   			else if(a == b)
   			{
   				ans+=a;
   				a=0;
   			}
   			else if(a < b)
   			{
   				ll t = b / a;
   				ans+=t;
   				t = b;
   				b = a;
   				a=t%a;
   			}
   		}
   		printf("%lld\n", ans);
   	}
   	return 0;
   }