hdu 4111 Alice and Bob(博弈)

hdu 4111 Alice and Bob(博弈)

題目鏈接：hdu 4111 Alice and Bob

題目大意；Alice和Bob兩個玩游戲，有N堆石子，每次可以從一堆中取走一個石子，或者是合並兩堆石子，Alice先，問

說最後誰贏。

解題思路：NP定理，寫出一些NP定理找到規律，再用歸納的方法證明。

統計1的個數c，以及非1情況下的步數s，包括合並。

• c為奇數，s不等於2：那麼先手必勝。
• s為2或者為0：c為3的倍數是先手必敗。
• 否則的話，s為奇數時先手必勝。

  首先沒有1的情況下很好證明，就是總的步數和為奇數時為先手必勝態，N點。相反，如果為偶數就是P點。（這種情況

  下必勝的人只要保證任意一堆石子的個數不會小於2即可，直到最後只剩下一堆，因為1是一個比較特殊的存在）
  

  再者證明奇數個1且s不為2的時候為必勝態，從一個1的開始，假設現在有一個1和s，如果s為奇數，那麼先手可以合並

  兩堆石子；如果s是偶數，先手可以拿走1；所以這種情況下一定是先手必勝，因為移動1可以選擇少掉一步或者兩步。

  那麼現在就是兩個1和s的情況，如果其中一個人先消耗掉一個1，和s合並，那麼剩下的狀態是(1,s+1)的N點；取走1，

  剩下(1,s)同樣是N點；合並兩個1，(2,s)==>(s+3)的狀態，如果s為奇數，那麼即為P態，對應的剛才先手就是必勝，反之

  則是必敗，這種情況歸納到結論中的第三條。那麼三個1的情況下就可以消耗一個1更變s的奇偶性。
  

  不過在s=2或者s=0的時候屬於特殊情況，因為2去掉一個之後就變成了1，s為0時為全1，通過上面的規律，我們已經知

  道了1是比較特殊的。那麼現在有NP圖
  
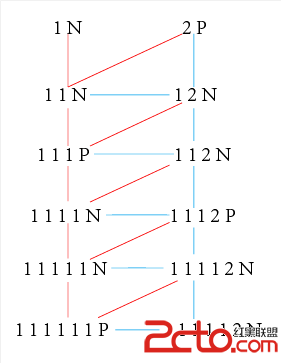
  不難發現，這是c如果是3的倍數，那麼一定是先手必敗態。

  #include 
  #include 
  #include 
  
  using namespace std;
  
  bool judge (int c, int s) {
      if (c&1 && s > 2)
          return true;
  
      if (s == 0 || s == 2)
          return c % 3;
      return s&1;
  }
  
  int main () {
      int cas;
      scanf("%d", &cas);
      for (int kcas = 1; kcas <= cas; kcas++) {
          int n, s = 0, c = 0, x;
  
          scanf("%d", &n);
          for (int i = 0; i < n; i++) {
              scanf("%d", &x);
              if (x == 1)
                  c++;
              else {
                  if (s == 0)
                      s = x;
                  else
                      s += x + 1;
              }
          }
          printf("Case #%d: %s\n", kcas, judge(c, s) ? "Alice" : "Bob");
      }
      return 0;
  }