程式師世界 >> 編程語言 >> C語言 >> C++ >> C++入門知識 >> POJ 1673 EXOCENTER OF A TRIANGLE（求三角形的垂心）

POJ 1673 EXOCENTER OF A TRIANGLE（求三角形的垂心）

編輯：C++入門知識

POJ 1673 EXOCENTER OF A TRIANGLE（求三角形的垂心）

EXOCENTER OF A TRIANGLE

題目大意:一個三角形，以它的每一條邊為邊各畫一個正方形，將各正方形的頂點連起來，將連線的中點與三角形的頂點分別相連並延長，延長線交於一點，求交點的坐標。

如圖：

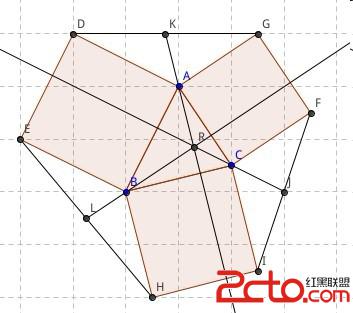
解題思路：其實這個題代碼不是很長，就是求三角形的垂心，但關鍵的問題就是怎麼證明這個交點是三角形的垂心。

這就需要作輔助線了，作A點關於K點的對稱點A'，連接A'D、A'K，如圖。

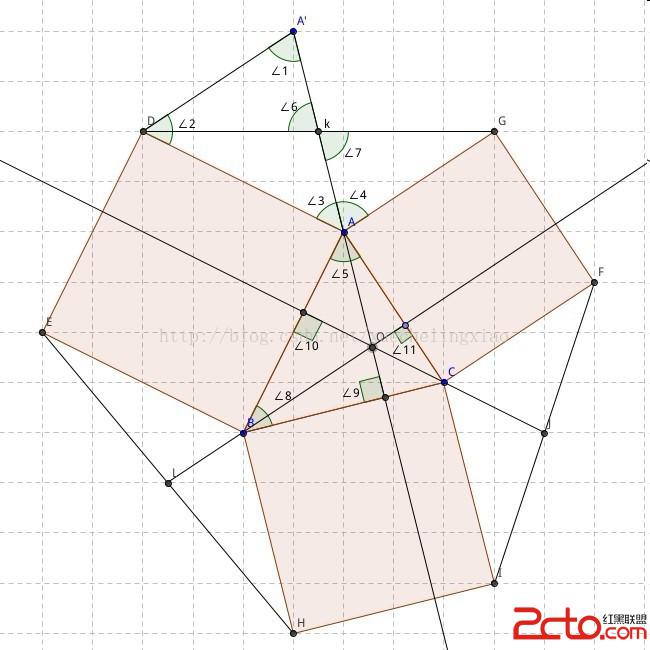
證明：

∵AK = A'K DK = GK ∠6 = ∠7

根據(SAS) ∴△AGK≌A'GK

∴∠1 = ∠4

又∵∠1 + ∠2 + ∠3 = 180°

∴∠2 + ∠3 + ∠4 = 180°

又∵∠3 + ∠4 + ∠5

∴∠2 = ∠5

又∵AD = AB AG = AC

根據SAS ∴△ABC≌DAA'

∴∠3 = ∠8

又∵∠BAO + ∠3 = 90°

∴∠BAO + ∠8 = 90°

∴∠9 = 90°

同理∠10 = ∠11 = 90°

∴點O為高線交點為△ABC的垂心

證畢。

具體的代碼部分就沒有什麼了

下面是代碼：

#include

#include #include #include #include #include #include #include #include #include #include #include #define LL long long //#define LL long long #define max(a,b) ((a)>(b)?(a):(b)) #define min(a,b) ((a)<(b)?(a):(b)) using namespace std; struct Point { double x, y; } A, B, C; struct Line { Point a, b; } ; Point intersection(Line u, Line v) { Point ret = u.a; double t = ((u.a.x-v.a.x)*(v.a.y-v.b.y) -(u.a.y-v.a.y)*(v.a.x-v.b.x)) /((u.a.x-u.b.x)*(v.a.y-v.b.y) -(u.a.y-u.b.y)*(v.a.x-v.b.x)); ret.x += (u.b.x-u.a.x)*t; ret.y += (u.b.y-u.a.y)*t; return ret; } Point perpencenter(Point a, Point b, Point c) { Line u, v; u.a = c; u.b.x = u.a.x-a.y+b.y; u.b.y = u.a.y+a.x-b.x; v.a = b; v.b.x = v.a.x-a.y+c.y; v.b.y = v.a.y+a.x-c.x; return intersection(u, v); } char s[1000010]; int main() { int T; scanf(%d, &T); while(T--) { scanf(%lf%lf%lf%lf%lf%lf, &A.x, &A.y, &B.x, &B.y, &C.x, &C.y); //printf(%lf %lf %lf %lf %lf %lf , A.x, A.y, B.x, B.y, C.x, C.y); Point ans = perpencenter(A, B, C); printf(%.4lf %.4lf , ans.x, ans.y); } return 0; }