程式師世界 >> 編程語言 >> C語言 >> C++ >> C++入門知識 >> UVA 11889-Benefit(數學_快速枚舉因子)

UVA 11889-Benefit(數學_快速枚舉因子)

編輯：C++入門知識

UVA 11889-Benefit(數學_快速枚舉因子)

Recently Yaghoub is playing a new trick to sell some more. When somebody gives him A Tomans, he who never has appropriate changes, asks for B Tomans such that lowest common multiple of A and B equals to C and he will pay back a round bill. Or otherwise take some snack instead of the remaining of his money. He believes that finding such a number is hard enough that dissuades students from paying that.

You should write a program that help poor students giving the appropriate amount of money to Yaghoub. Of course if there are several answers you go for students' benefit which is the lowest of them.

Input

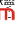
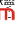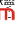
The first line begin with an integer T ( T $\le$ 100000), the number of tests. Each test that comes in a separate line contains two integers A and C ( 1 $\le$ A, C $\le$ 10⁷).

Output

Print the lowest integer B such that LCM(A, B) = C in a single line. If no such integer exists, print "NO SOLUTION" instead. (Quotes for clarity)

Sample Input

Sample Output

3
55
NO SOLUTION

題意 ：很簡單 給出a，c求滿足 lcm(a,b)==c 的最小整數b。沒有則輸出“NO SOLUTION”。

lcm(a,b)==a*b/gcd(a,b)==c --> a*b==gcd(a,b)*c; --> a/gcd(a,b)==c/b,因為a/gcd(a,b)肯定為整數，所以b肯定是c的因子，枚舉c的因子即可。

一開始純暴力枚舉c的因子T了一發，才明白數學果然是王道。 枚舉因子在判斷素數的時候就有過優化，即只需要枚舉到sqrt(c)。 還有一個優化條件是a必須是c的因子。因為

b/gcd(a,b)==c/a;

#include 
#include 
#include 
#include 
#include 
#include 
#include 
#include 
#include 
#include 
#include 
#include 
#define ll long long
using namespace std;
const int INF = 0x3f3f3f3f;
ll gcd(ll a,ll b)
{
	if(b==0) return a;
	else return gcd(b,a%b);
}
void solve(ll a,ll c)
{
	// b/gcd(a,b)==c/a
	if(c%a)
	{
		puts("NO SOLUTION");
		return ;
	}
	ll b=1,ans=INF;
	int m=floor(sqrt(c)+0.5);
	while(b<=m)
	{
		if(c%b==0)
		{
			if(a*b==c*gcd(a,b))
			{
				ans=min(ans,b);
				break;
			}
			ll sb=c/b;
			if(a*sb==c*gcd(a,sb))
				ans=min(ans,sb);
		}
		b++;
	}
	if(ans!=INF)
		printf("%lld\n",ans);
	else
		puts("NO SOLUTION");
}
int main()
{
	int t;ll a,b,c;
	scanf("%d",&t);
	//   a/gcd(a,b)==c/b;
	while(t--)
	{
		scanf("%lld%lld",&a,&c);
		solve(a,c);
	}
	return 0;
}