程式師世界 >> 編程語言 >> C語言 >> C++ >> C++入門知識 >> hdu5073 2014鞍山現場賽D題

hdu5073 2014鞍山現場賽D題

編輯：C++入門知識

hdu5073 2014鞍山現場賽D題

Galaxy

Time Limit: 2000/1000 MS (Java/Others) Memory Limit: 262144/262144 K (Java/Others)
Total Submission(s): 1421 Accepted Submission(s): 324
Special Judge

Problem Description Good news for us: to release the financial pressure, the government started selling galaxies and we can buy them from now on! The first one who bought a galaxy was Tianming Yun and he gave it to Xin Cheng as a present.

To be fashionable, DRD also bought himself a galaxy. He named it Rho Galaxy. There are n stars in Rho Galaxy, and they have the same weight, namely one unit weight, and a negligible volume. They initially lie in a line rotating around their center of mass.

Everything runs well except one thing. DRD thinks that the galaxy rotates too slow. As we know, to increase the angular speed with the same angular momentum, we have to decrease the moment of inertia.

The moment of inertia I of a set of n stars can be calculated with the formula

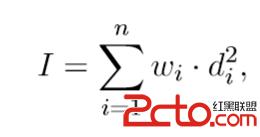
where w_i is the weight of star i, d_i is the distance form star i to the mass of center.

As DRD’s friend, ATM, who bought M78 Galaxy, wants to help him. ATM creates some black holes and white holes so that he can transport stars in a negligible time. After transportation, the n stars will also rotate around their new center of mass. Due to financial pressure, ATM can only transport at most k stars. Since volumes of the stars are negligible, two or more stars can be transported to the same position.

Now, you are supposed to calculate the minimum moment of inertia after transportation.
Input The first line contains an integer T (T ≤ 10), denoting the number of the test cases.

For each test case, the first line contains two integers, n(1 ≤ n ≤ 50000) and k(0 ≤ k ≤ n), as mentioned above. The next line contains n integers representing the positions of the stars. The absolute values of positions will be no more than 50000.
Output For each test case, output one real number in one line representing the minimum moment of inertia. Your answer will be considered correct if and only if its absolute or relative error is less than 1e-9.
Sample Input

Sample Output

0
0.5

Source 2014 Asia AnShan Regional Contest

題意：數軸上n個點，可以任意移動k個點，要使得移動後的數的方差最小，問最小的值是多少。

分析：首先可以想到要移動的點肯定是兩端的某些點，也就是剩下的點是連續的，而且移動後的位置肯定是剩下的點平均位置的地方。這樣其實我們就枚舉連續的n-k個數的起點，求這些數的方差即可。

如果是n^2去求肯定會超時，這裡注意到(xi-x')^2=xi^2+x'^2-2*x*x'(x'是平均數)，我們就維護一個連續n-k個數的平方和以及和,到下一個點時類似滑動窗口一加一減就可以算出此時的平方和以及和。那麼最後的方差就等於sum(x^2)+(sum(x)/m)^2*m-2*sum(x)*sum(x)/m

化簡下就是sum(x^2)-sum(x)*sum(x)/m。注意特判n-k為0的情況。

/**
 * @author neko01
 */
//#pragma comment(linker, /STACK:102400000,102400000)
#include 
#include 
#include 
#include 
#include 
#include 
#include 
#include 
#include 
#include
using namespace std;
typedef long long LL;
#define min3(a,b,c) min(a,min(b,c))
#define max3(a,b,c) max(a,max(b,c))
#define pb push_back
#define mp(a,b) make_pair(a,b)
#define clr(a) memset(a,0,sizeof a)
#define clr1(a) memset(a,-1,sizeof a)
#define dbg(a) printf(%d
,a)
typedef pair pp;
const double eps=1e-9;
const double pi=acos(-1.0);
const int INF=0x3f3f3f3f;
const LL inf=(((LL)1)<<61)+5;
const int N=50005;
double a[N];
int main()
{
    int n,k,t;
    scanf(%d,&t);
    while(t--)
    {
        scanf(%d%d,&n,&k);
        for(int i=1;i<=n;i++)
        {
            scanf(%lf,&a[i]);
        }
        sort(a+1,a+1+n);
        int m=n-k;
        if(m==0)
        {
            puts(0);
            continue;
        }
        double ans,ave,s1=0,s2=0;
        for(int i=1;i<=m;i++)
        {
            s2+=a[i];
            s1+=a[i]*a[i];
        }
        ans=s1-s2*s2/m;
        for(int i=1;i<=k;i++)
        {
            s1=s1-a[i]*a[i]+a[i+m]*a[i+m];
            s2=s2-a[i]+a[i+m];
            ans=min(ans,s1-s2*s2/m);
        }
        printf(%.9f
,ans);
    }
    return 0;
}