現在有一塊X*Y的矩形布條, 然後有n種規格的x[i]*y[i]的小布條, 每種布條可以賣出val[i]的價值. 問你原始的X*Y布條最多能賣多少價值? 其中每次切割布條只能水平或垂直的切, 且一刀到底.
分析:
本題看起來比較麻煩, 但是搞懂原理後還是很簡單的. 把當前還剩余的矩形布條看成容量, 那麼我們就是再這有限的容量裡面要找出最大價值的布條總和來.
令dp[i][j]==x 表示當前長i和寬j的布條能切割出的最大價值為x.
這裡有個結論要注意: 我們每次從大矩形中切割出一個小矩形, 總是沿著大矩形的頂角邊緣切割將不會丟失最優解.
比如一個i*j的大矩形, 我們如果要從中切割出一個x*y的小矩形, 有下面4種方式(大矩形可以選擇先下垂直那刀或先下水平那刀, 小矩形能旋轉):
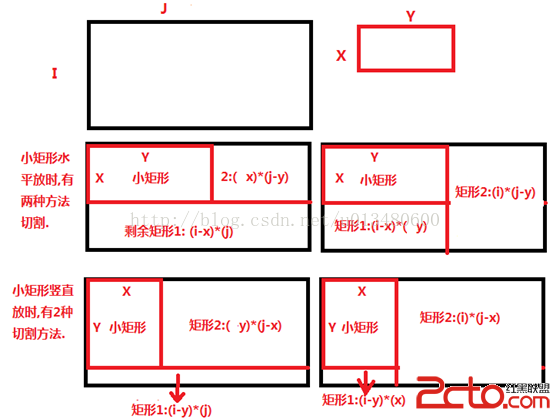
(仔細體會上面這個圖.)
有了上面的圖, 下面我們的遞推公式就出來了:
if(i>=r[k].x&& j>=r[k].y)
dp[i][j]=max(dp[i][j] , max( dp[i-r[k].x][j]+dp[r[k].x][j-r[k].y] ,dp[i-r[k].x][r[k].y]+dp[i][j-r[k].y] )+r[k].val );
if(i>=r[k].y && j>=r[k].x)
dp[i][j]=max(dp[i][j] , max( dp[r[k].y][j-r[k].x]+dp[i-r[k].y][j] ,dp[i-r[k].y][r[k].x]+dp[i][j-r[k].x] )+r[k].val );
上面兩個公式好像看起來很復雜, 其實理解上面的圖之後就很簡單了. 本質就是:
原始矩形能獲得的最大價值 == max(小矩形價值 + 被水平一刀和豎直一刀切割後剩下的兩個矩形能獲得的最大價值和 )
也就是求切割後的3個矩形的價值和, 看看哪種方式切割剩下的矩形價值和最大.(兩刀之後, 原始矩形必然變成3個新矩形)
初始化: dp為全0.
最終所求: dp[X][Y].
注意: 完全背包問題限制條件的維度j和物品編號的維度i的循環先後順序是可以互換的. 但是此題必須先循環X和Y的維度, 然後才是物品編號的維度. 因為一般的完全背包問題的最優解對於物品的選取順序沒有要求, 可以先區任何物品. 但是此題對於原始矩形來說, 你在它的頂角邊緣先切割那個小矩形是明顯不同的,有可能你先切割1號矩形就得不到最優解, 但是你先切割3號矩形才能得到最優解(仔細想想是不是).
AC代碼:
#include#include #include using namespace std; const int maxn=1000+5; int X,Y;//原始矩形寬和高 int n; //有多少個小布條 struct Node//每個小布條 { int x,y; int val; }r[10+5]; int dp[maxn][maxn]; int main() { int T; scanf(%d,&T); while(T--) { //讀取輸入+初始化 scanf(%d%d%d,&n,&X,&Y); for(int i=1;i<=n;i++) scanf(%d%d%d,&r[i].x,&r[i].y,&r[i].val); memset(dp,0,sizeof(dp)); //遞推,注意:先X和Y,然後才是矩形編號. //如果先循環矩形編號,就錯了. for(int i=0;i<=X;i++) for(int j=0;j<=Y;j++) for(int k=1;k<=n;k++) { if(i>=r[k].x && j>=r[k].y) dp[i][j]=max( dp[i][j] , max( dp[i-r[k].x][j]+dp[r[k].x][j-r[k].y] , dp[i-r[k].x][r[k].y]+dp[i][j-r[k].y] )+r[k].val ); if(i>=r[k].y && j>=r[k].x) dp[i][j]=max( dp[i][j] , max( dp[r[k].y][j-r[k].x]+dp[i-r[k].y][j] , dp[i-r[k].y][r[k].x]+dp[i][j-r[k].x] )+r[k].val ); } //輸出結果 printf(%d ,dp[X][Y]); } }