在計算機科學中,trie,又稱前綴樹或字典樹或單詞搜索樹,是一種有序樹,用於保存關聯數組,其中的鍵通常是字符串。與二叉查找樹不同,鍵不是直接保存在節點中,而是由節點在樹中的位置決定。一個節點的所有子孫都有相同的前綴,也就是這個節點對應的字符串,而根節點對應空字符串。一般情況下,不是所有的節點都有對應的值,只有葉子節點和部分內部節點所對應的鍵才有相關的值。
本文地址:http://www.cnblogs.com/archimedes/p/trie-tree.html,轉載請注明源地址。
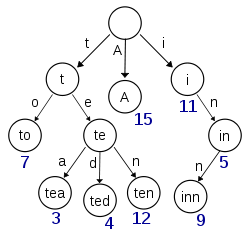
在圖示中,鍵標注在節點中,值標注在節點之下。每一個完整的英文單詞對應一個特定的整數。Trie 可以看作是一個確定有限狀態自動機,盡管邊上的符號一般是隱含在分支的順序中的。鍵不需要被顯式地保存在節點中。圖示中標注出完整的單詞,只是為了演示 trie 的原理。
trie 中的鍵通常是字符串,但也可以是其它的結構。trie 的算法可以很容易地修改為處理其它結構的有序序列,比如一串數字或者形狀的排列。比如,bitwise trie 中的鍵是一串位元,可以用於表示整數或者內存地址。
Trie樹是一種樹形結構,是一種哈希樹的變種。典型應用是用於統計和排序大量的字符串(但不僅限於字符串),所以經常被搜索引擎系統用於文本詞頻統計。它的優點是:最大限度地減少無謂的字符串比較,查詢效率比哈希表高。Trie的核心思想是空間換時間。利用字符串的公共前綴來降低查詢時間的開銷以達到提高效率的目的。
它有3個基本性質:
(1) 根節點不包含字符,除根節點外每一個節點都只包含一個字符。
(2) 從根節點到某一節點,路徑上經過的字符連接起來,為該節點對應的字符串。
(3) 每個節點的所有子節點包含的字符都不相同。
基本思想(以字母樹為例):
1、插入過程
對於一個單詞,從根開始,沿著單詞的各個字母所對應的樹中的節點分支向下走,直到單詞遍歷完,將最後的節點標記為紅色,表示該單詞已插入Trie樹。
2、查詢過程
同樣的,從根開始按照單詞的字母順序向下遍歷trie樹,一旦發現某個節點標記不存在或者單詞遍歷完成而最後的節點未標記為紅色,則表示該單詞不存在,若最後的節點標記為紅色,表示該單詞存在。
字母樹的插入(Insert)、刪除( Delete)和查找(Find)都非常簡單,用一個一重循環即可,即第i 次循環找到前i個字母所對應的子樹,然後進行相應的操作。實現這棵字母樹,至於Trie樹的實現,可以用數組,也可以用指針動態分配,平時為了方便就用數組,靜態分配空間。
1、trie結構體
struct Trie
{
Trie *next[26];
bool isWord;
}Root;
2、插入操作
//插入操作(也是構建Trie樹)
void insert(char *tar)
{
Trie* head = &Root;
int id;
while(*tar)
{
id = *tar - 'a';
if(head->next[id] == NULL)
head->next[id] = new Trie();
head = head->next[id];
tar++;
}
head->isWord = true;
}
3、查找操作
//查找
bool search(char *tar)
{
Trie* head = &Root;
int id;
while(*tar)
{
id = *tar - 'a';
if(head->next[id] == NULL)
return false;
head = head->next[id];
tar++;
}
if(head->isWord)
return true;
else
return false;
}
至於結點對兒子的指向,一般有三種方法:
1、對每個結點開一個字母集大小的數組,對應的下標是兒子所表示的字母,內容則是這個兒子對應在大數組上的位置,即標號;
2、對每個結點掛一個鏈表,按一定順序記錄每個兒子是誰;
3、使用左兒子右兄弟表示法記錄這棵樹。
三種方法,各有特點。第一種易實現,但實際的空間要求較大;第二種,較易實現,空間要求相對較小,但比較費時;第三種,空間要求最小,但相對費時且不易寫。
下面給出動態開辟內存的實現:
#define MAX_NUM 26
enum NODE_TYPE{ //"COMPLETED" means a string is generated so far.
COMPLETED,
UNCOMPLETED
};
struct Node {
enum NODE_TYPE type;
char ch;
struct Node* child[MAX_NUM]; //26-tree->a, b ,c, .....z
};
struct Node* ROOT; //tree root
struct Node* createNewNode(char ch){
// create a new node
struct Node *new_node = (struct Node*)malloc(sizeof(struct Node));
new_node->ch = ch;
new_node->type == UNCOMPLETED;
int i;
for(i = 0; i < MAX_NUM; i++)
new_node->child[i] = NULL;
return new_node;
}
void initialization() {
//intiazation: creat an empty tree, with only a ROOT
ROOT = createNewNode(' ');
}
int charToindex(char ch) { //a "char" maps to an index<br>
return ch - 'a';
}
int find(const char chars[], int len) {
struct Node* ptr = ROOT;
int i = 0;
while(i < len) {
if(ptr->child[charToindex(chars[i])] == NULL) {
break;
}
ptr = ptr->child[charToindex(chars[i])];
i++;
}
return (i == len) && (ptr->type == COMPLETED);
}
void insert(const char chars[], int len) {
struct Node* ptr = ROOT;
int i;
for(i = 0; i < len; i++) {
if(ptr->child[charToindex(chars[i])] == NULL) {
ptr->child[charToindex(chars[i])] = createNewNode(chars[i]);
}
ptr = ptr->child[charToindex(chars[i])];
}
ptr->type = COMPLETED;
}
Trie是一種非常簡單高效的數據結構,但有大量的應用實例。
(1) 字符串檢索
事先將已知的一些字符串(字典)的有關信息保存到trie樹裡,查找另外一些未知字符串是否出現過或者出現頻率。
舉例:
1、給出N個單詞組成的熟詞表,以及一篇全用小寫英文書寫的文章,請你按最早出現的順序寫出所有不在熟詞表中的生詞。
2、給出一個詞典,其中的單詞為不良單詞。單詞均為小寫字母。再給出一段文本,文本的每一行也由小寫字母構成。判斷文本中是否含有任何不良單詞。例如,若rob是不良單詞,那麼文本problem含有不良單詞。
(2)字符串最長公共前綴
Trie樹利用多個字符串的公共前綴來節省存儲空間,反之,當我們把大量字符串存儲到一棵trie樹上時,我們可以快速得到某些字符串的公共前綴。
舉例:
給出N 個小寫英文字母串,以及Q 個詢問,即詢問某兩個串的最長公共前綴的長度是多少?
解決方案:首先對所有的串建立其對應的字母樹。此時發現,對於兩個串的最長公共前綴的長度即它們所在結點的公共祖先個數,於是,問題就轉化為了離線(Offline)的最近公共祖先(Least Common Ancestor,簡稱LCA)問題。
而最近公共祖先問題同樣是一個經典問題,可以用下面幾種方法:
1. 利用並查集(Disjoint Set),可以采用采用經典的Tarjan 算法;
2. 求出字母樹的歐拉序列(Euler Sequence )後,就可以轉為經典的最小值查詢(Range Minimum Query,簡稱RMQ)問題了;
(3)排序
Trie樹是一棵多叉樹,只要先序遍歷整棵樹,輸出相應的字符串便是按字典序排序的結果。
舉例:
給你N 個互不相同的僅由一個單詞構成的英文名,讓你將它們按字典序從小到大排序輸出。
(4) 作為其他數據結構和算法的輔助結構
如後綴樹,AC自動機等
#define MAX 26 //字符集大小
typedef struct TrieNode
{
int nCount; //記錄該字符出現次數
struct TrieNode *next[MAX];
}TrieNode;
TrieNode Memory[1000000];
int allocp = 0;
/*初始化*/
void InitTrieRoot(TrieNode **pRoot)
{
*pRoot = NULL;
}
/*創建新結點*/
TrieNode *CreateTrieNode()
{
int i;
TrieNode *p;
p = &Memory[allocp++];
p->nCount = 1;
for(i = 0 ; i < MAX ; i++)
p->next[i] = NULL;
return p;
}
/*插入*/
void InsertTrie(TrieNode **pRoot , char *s)
{
int i , k;
TrieNode *p;
if(!(p = *pRoot))
p = *pRoot = CreateTrieNode();
i = 0;
while(s[i]) {
k = s[i++] - 'a'; //確定branch
if(p->next[k])
p->next[k]->nCount++;
else
p->next[k] = CreateTrieNode();
p = p->next[k];
}
}
//查找
int SearchTrie(TrieNode **pRoot , char *s)
{
TrieNode *p;
int i , k;
if(!(p = *pRoot))
return 0;
i = 0;
while(s[i]) {
k = s[i++] - 'a';
if(p->next[k] == NULL) return 0;
p = p->next[k];
}
return p->nCount;
}
字典樹(trie tree)
Trie樹就是字典樹,其核心思想就是空間換時間。
舉個簡單的例子。
給你100000個長度不超過10的單詞。對於每一個單詞,我們要判斷他出沒出現過,如果出現了,第一次出現第幾個位置。
這題當然可以用hash來,但是我要介紹的是trie樹。在某些方面它的用途更大。比如說對於某一個單詞,我要詢問它的前綴是否出現過。這樣hash就不好搞了,而用trie還是很簡單。
現在回到例子中,如果我們用最傻的方法,對於每一個單詞,我們都要去查找它前面的單詞中是否有它。那麼這個算法的復雜度就是O(n^2)。顯然對於100000的范圍難以接受。現在我們換個思路想。假設我要查詢的單詞是abcd,那麼在他前面的單詞中,以b,c,d,f之類開頭的我顯然不必考慮。而只要找以a開頭的中是否存在abcd就可以了。同樣的,在以a開頭中的單詞中,我們只要考慮以b作為第二個字母的……這樣一個樹的模型就漸漸清晰了……
假設有b,abc,abd,bcd,abcd,efg,hii這6個單詞,我們構建的樹就是這樣的。
對於每一個節點,從根遍歷到他的過程就是一個單詞,如果這個節點被標記為紅色,就表示這個單詞存在,否則不存在。
那麼,對於一個單詞,我只要順著他從跟走到對應的節點,再看這個節點是否被標記為紅色就可以知道它是否出現過了。把這個節點標記為紅色,就相當於插入了這個單詞。
這樣一來我們詢問和插入可以一起完成,所用時間僅僅為單詞長度,在這一個樣例,便是10。
我們可以看到,trie樹每一層的節點數是26^i級別的。所以為了節省空間。我們用動態鏈表,或者用數組來模擬動態。空間的花費,不會超過單詞數×單詞長度。
字典樹(Trie)是一種用於快速字符串檢索的多叉樹結構。其原理是利用字符串的公共前綴來降低時空開銷,從而達到提高程序效率的目的。
它有如下簡單的性質: (1) 根節點不包含字符信息; (3) 一棵m度的Trie或者為空,或者由m棵m度的Trie組成。 搜索字典項目的方法為: (1) 從根結點開始一次搜索; (2) 取得要查找關鍵詞的第一個字母,並根據該字母選擇對應的子樹 並轉到該子樹繼續進行檢索; (3) 在相應的子樹上,取得要查找關鍵詞的第二個字母, 並進一步選擇對應的子樹進行檢索。 (4) 迭代過程…… (5) 在某個結點處,關鍵詞的所有字母已被取出,則讀取 附在該結點上的信息,即完成查找。
附上AC代碼供樓主好好研究
#include<stdio.h>
#include<stdlib.h>
#include<string.h>
struct dictree
{
struct dictree *child[26];
int n;
};
struct dictree *root;
void insert(char *source)
{
int len,i,j;
struct dictree *current,*newnode;
len=strlen(source);
if(len==0) return ;
current=root;
for(i=0;i<len;i++){
if(current->child[source[i]-'a'......余下全文>>
字典樹(Trie樹),
Trie樹是字典樹,其核心思想是空間換時間。
對於一個簡單的例子。
給你10萬長度不超過10個字。對於每一個單詞,我們要判斷他來來去去,如果有,第一次出現了幾個位置。
當然,這個問題可以使用哈希來,但我要為大家介紹trie樹。其使用在一些方面中更大。例如,對於一個字,我要問它是否是一個前綴出現。這樣的哈希值不從事特裡還是很簡單的。
現在回去的例子,如果我們用最笨的辦法,為每個詞,我們不得不去尋找它前面的字是否。該算法的復雜性為O(n ^ 2)。顯然,對於100000的范圍難以接受。現在,我們要換個思路。假設我必須要找到這個詞ABCD,那麼這個詞在他的面前,B,C,D,F和像開始時,我顯然不加以考慮。只需要找到是否有ABCD的一個開端。同樣,在開頭的詞,只要我們考慮到B的第二個字母...這種樹的模型逐漸清晰......
假設B,ABC,ABD,BCD ABCD,EFG,HII六個字,我們建立了樹。
對於每個節點遍歷的過程從根本上就是一個字,這個字被認為存在或不存在,如果節點被標記為紅色。
好了,一個字,我只是跟著他了相應的節點,在這個節點被標記為紅色就可以知道它之前出現。這個節點被標記為紅色,相當於這個詞被插入。
所以我們要求的時間,只是這個詞的長度和插入就可以完成,在樣品中,有10。
我們可以看到,每一層的trie樹中的節點是26 ^ I級,。因此,為了以節省空間。我們使用了動態鏈接列表,或模擬動態數組。的空間,字長的成本不超過的字的數量。
詞典樹(特裡)是一種快速字符串搜索多樹結構。其原理是使用一個共同的前綴字符串,以減少時間和空間的開銷,從而提高程序的效率要達到的目的。
它具有以下簡單的特性:(1)根節點包含字符信息;(3)的m度特裡是空的,或者米的樹木M度特裡。查詢項目:(1)從根節點開始搜索;(2)獲取信要查找的關鍵字,選擇相應的子樹,並按照信中的子樹繼續被檢索( 3)在相應的子樹,你要查找的關鍵字並選擇相應的子樹檢索的第二個字母。 (4)迭代過程...... (5)在一個路口,已被刪除的關鍵字的所有字母,然後讀取的信息連接的結點,即完成搜索。
附加的AC代碼房東良好的學習
#包括
#包括
#中
結構dictree
{
結構dictree *子[26];
整數N;
} dictree *根;
無效插入(CHAR *源)
{
INT鏡頭,I,J;
dictree *電流* newnode; BR />長度= strlen的(源);
(LEN == 0)返回
電流=根;
(i = 0; <LEN,我+ +){
(電流>子[I] - [來源'一'] = 0){
電流=電流>子源[I] - 'A'];
CURRENT-> N =電流> N +1;
}
其他{
newnode =(dictree *)的malloc(sizeof(結構dictree))的;
(J = 0; J <26; + +)
newnode->子[J] = 0;
電流>子[I] - [來源'一'] = newnode;
電流= newnode;
電流> N = 1;
}
}
}
INT找到(字符*源)
{
我,LEN;
結構dictree *電流;
長度= strlen的(源);
(LEN == 0)返回0;
電流=根;......余下全文>>