[ACM] hdu 3549 Flow Problem （最大流模板題）

Flow Problem

Problem Description Network flow is a well-known difficult problem for ACMers. Given a graph, your task is to find out the maximum flow for the weighted directed graph.
Input The first line of input contains an integer T, denoting the number of test cases.
For each test case, the first line contains two integers N and M, denoting the number of vertexes and edges in the graph. (2 <= N <= 15, 0 <= M <= 1000)
Next M lines, each line contains three integers X, Y and C, there is an edge from X to Y and the capacity of it is C. (1 <= X, Y <= N, 1 <= C <= 1000)
Output For each test cases, you should output the maximum flow from source 1 to sink N.
Sample Input

2
3 2
1 2 1
2 3 1
3 3
1 2 1
2 3 1
1 3 1

Sample Output

Case 1: 1
Case 2: 2

Author HyperHexagon
Source HyperHexagon's Summer Gift (Original tasks)

解題思路：

本題為赤裸裸的最大流模板題。Ford-Fulkerson方法

其中為什麼要用到殘留網絡，不好理解。

下面講解有所啟發，轉載於：http://www.cnblogs.com/acSzz/archive/2012/09/13/2683820.html

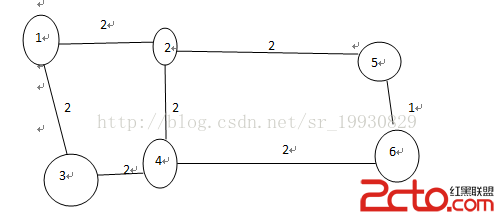
必須使用反向弧的流網絡

在這幅圖中我們首先要增廣1->2->4->6,這時可以獲得一個容量為 2的流,但是如果不建立4->2反向弧的話,則無法進一步增廣,最終答案為2,顯然是不對的,然而如果建立了反向弧4->2,則第二次能進行 1->3->4->2->5->6的增廣,最大流為3.

Comzyh對反向弧的理解可以說是"偷梁換柱",請仔細閱讀: 在上面的例子中,我們可以看出,最終結果是1->2->5->6和1->2->4->6和 1->3->4->6.當增廣完1->2->4->6(代號A)後,在增廣 1->3->4->2->5->6(代號B),相當於將經過節點2的A流從中截流1(總共是2)走2->5>6,而不走2->4>6了,同時B流也從節點4截流出1(總共是1)走4->6而不是4->2->5->6,相當於AB流做加法.

代碼：

#include 
#include 
#include 
#include 
#include 
using namespace std;
using namespace std;
const int maxn=20;
const int inf=0x3f3f3f3f;
int pre[maxn];   //保存前驅節點
bool vis[maxn];
int mp[maxn][maxn];//臨接矩陣保存殘留網絡

int s,e;//s為源點，e為匯點
int n,m;//輸入n個頂點，m條邊

bool bfs()
{
    queueq;
    memset(pre,0,sizeof(pre));
    memset(vis,0,sizeof(vis));
    vis[s]=1;
    q.push(s);
    while(!q.empty())
    {
        int first=q.front();
        q.pop();
        if(first==e)
            return true;//找到一條增廣路
        for(int i=1;i<=n;i++)
        {
            if(!vis[i]&&mp[first][i])
            {
                q.push(i);
                pre[i]=first;
                vis[i]=1;
            }
        }
    }
    return false;
}

int max_flow()
{
    int ans=0;
    while(1)
    {
        if(!bfs())//找不到增廣路
            return ans;
        int Min=inf;
        for(int i=e;i!=s;i=pre[i])//回溯找最小流量
            Min=min(Min,mp[pre[i]][i]);
        for(int i=e;i!=s;i=pre[i])
        {
            mp[pre[i]][i]-=Min;
            mp[i][pre[i]]+=Min;
        }
        ans+=Min;
    }
}

int main()
{
    int t;
    scanf("%d",&t);
    int u,v,c;
    for(int cas=1;cas<=t;cas++)
    {
        scanf("%d%d",&n,&m);
        s=1,e=n;
        memset(mp,0,sizeof(mp));
        while(m--)
        {
            scanf("%d%d%d",&u,&v,&c);
            mp[u][v]+=c;
        }
        printf("Case %d: %d\n",cas,max_flow());
    }
    return 0;
}