記得剛學習C++那會這個問題曾困擾過我,後來慢慢形成了不管什麼時候都用一維數組的習慣,再後來知道了在一維數組中提出首列元素地址進行二維調用的辦法。可從來沒有細想過這個問題,最近自己寫了點代碼測試下,雖然還是有些不明就裡,不過結果挺有意思。
為了避免編譯器優化過度,用的是寫操作,int,測試分為不同大小的空間,同樣大小空間不同的行和列數。分別記錄逐行寫入,逐列寫入,按間隔寫入,空間申請和釋放的時間。
測試代碼
一維數組的申請和釋放
1 // Create 2 int *m = new int[n_row * n_col]; 3 4 // Free 5 delete [] m;
二維數組的申請和釋放
1 // Create 2 int **m = new int*[n_row]; 3 for ( int i = 0; i < n_row; ++i ) 4 m[i] = new int[n_col]; 5 6 // Free 7 for ( int i = 0; i < n_row; ++i ) 8 delete [] m[i]; 9 delete [] m;
逐行寫入
1 for ( int i = 0; i < n_row; ++i )
2 {
3 for ( int j = 0; j < n_col; ++j )
4 {
5 matrix[i * n_col + j] = answer;
6 // matrix[i][j] = answer;
7 }
8 }
逐列寫入
1 for ( int j = 0; j < n_col; ++j )
2 {
3 for ( int i = 0; i < n_row; ++i )
4 {
5 matrix[i * n_col + j] = answer;
6 // matrix[i][j] = answer;
7 }
8 }
按間隔寫入
1 for ( int i = 0; i < n_row; ++i )
2 {
3 for ( int j = 0; j < n_col; ++j )
4 {
5 int row = i * 7 % n_row;
6 int col = j * 11 % n_col;
7 matrix[i * n_col + j] = answer;
8 // matrix[i][j] = answer;
9 }
10 }
不是很確定這種測試是否很合理,不過大體上能體現我要測的東西了。需要注意的是逐行寫入中為了簡便我用的是寫入一個叫answer的變量,其實情況應該更泛化,否則用memset或者std::fill也許會更快?逐列寫入的代碼本科課程級別的典型反面代碼例子,這裡也僅僅是為了測試。
僅僅從編譯的角度來看主要的差別在下面兩句:
1 matrix[i * n_col + j] = answer; 2 matrix[i][j] = answer;
來看一下對應的匯編代碼:
1 ; matrix[i * n_col + j] = answer; 2 mov edx, DWORD PTR _i$3[ebp] 3 imul edx, DWORD PTR _n_col$[ebp] 4 add edx, DWORD PTR _j$2[ebp] 5 mov eax, DWORD PTR _matrix$[ebp] 6 mov ecx, DWORD PTR _answer$[ebp] 7 mov DWORD PTR [eax+edx*4], ecx
1 ; matrix[i][j] = answer; 2 mov ecx, DWORD PTR _i$4[ebp] 3 mov edx, DWORD PTR _matrix$[ebp] 4 mov eax, DWORD PTR [edx+ecx*4] 5 mov ecx, DWORD PTR _j$3[ebp] 6 mov edx, DWORD PTR _answer$[ebp] 7 mov DWORD PTR [eax+ecx*4], edx
都是6條指令,體系學得不好,所以也看不出哪個更快。這裡用的是Visual Studio編譯,因為本人gcc用得不熟,不知道怎麼生成這麼直觀的匯編和C++對應,效率上而言Linux下還是比Windows高一些,不過為了統一,之後的測試也基於Windows。當然上面的是沒有優化的編譯,如果開了優化(VS /O2),匯編指令大概也都是4、5條的樣子,因為/O2優化後的匯編代碼結構不是很直觀,這裡就不貼了。(另一方面也是由於我的匯編水平很弱,看不出什麼)
除了直接使用一維和二維數組,也可以對一維數組進行二維索引,方法是把一維數組中所有對應第一列的元素的地址單獨作為一個指針數組,這樣本質上還是一維數組,但是實現了形式上的二維數組調用,這種辦法空間申請的代碼如下:
1 // Create 2 int **m = new int*[n_row]; 3 int *block = new int[n_row * n_col]; 4 for ( int i = 0; i < n_row; ++i ) 5 m[i] = &block[i * n_col]; 6 return m;
釋放的代碼和二維數組相同。
用一維數組模擬二維調用的優點是既保證了內存空間的連續性,又保持了二維調用的代碼易維護的優點。不過需要注意的是,由於是二維索引,匯編代碼和二維數組還是一樣的。
測試結果
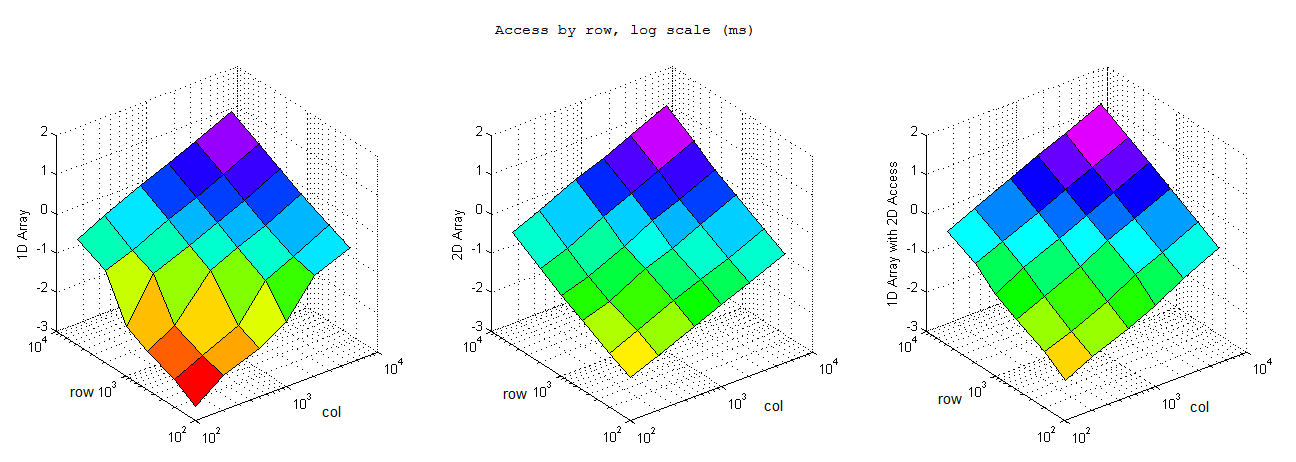
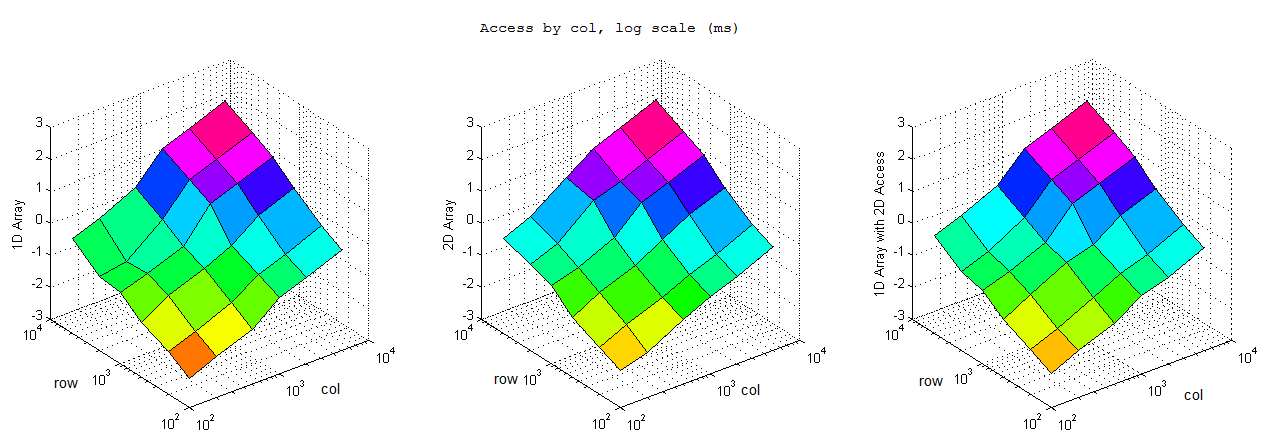
執行上面的代碼,在不同行數和列數下,循環執行取平均值,結果如下:
內存的申請和釋放:
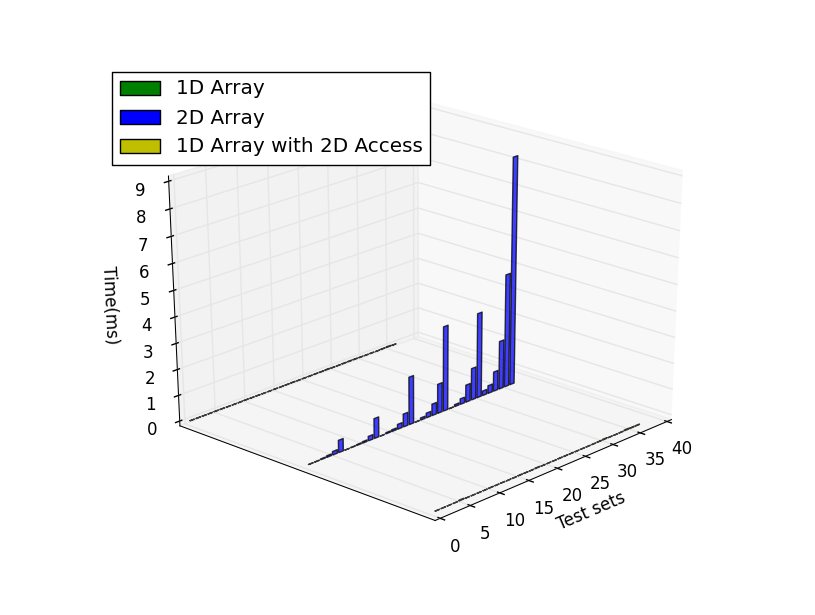
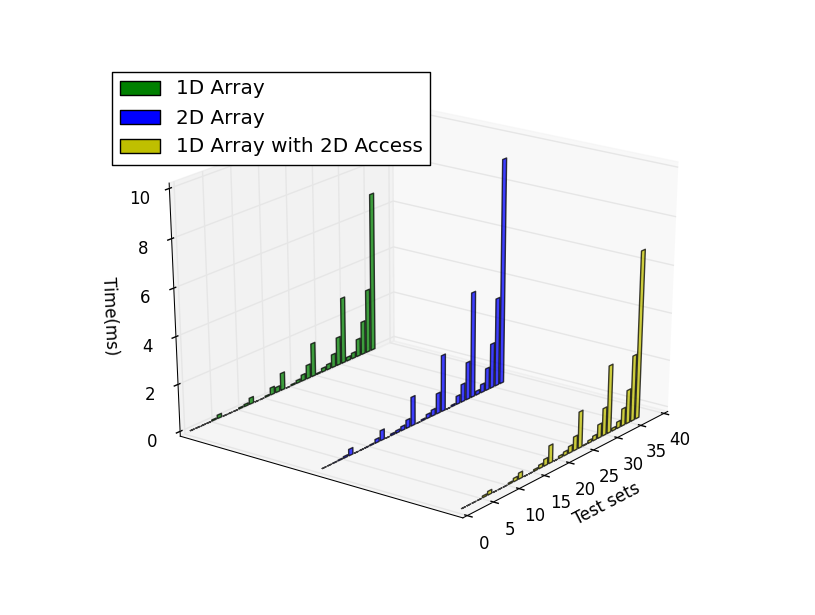
逐行訪問
逐列訪問
按間隔訪問
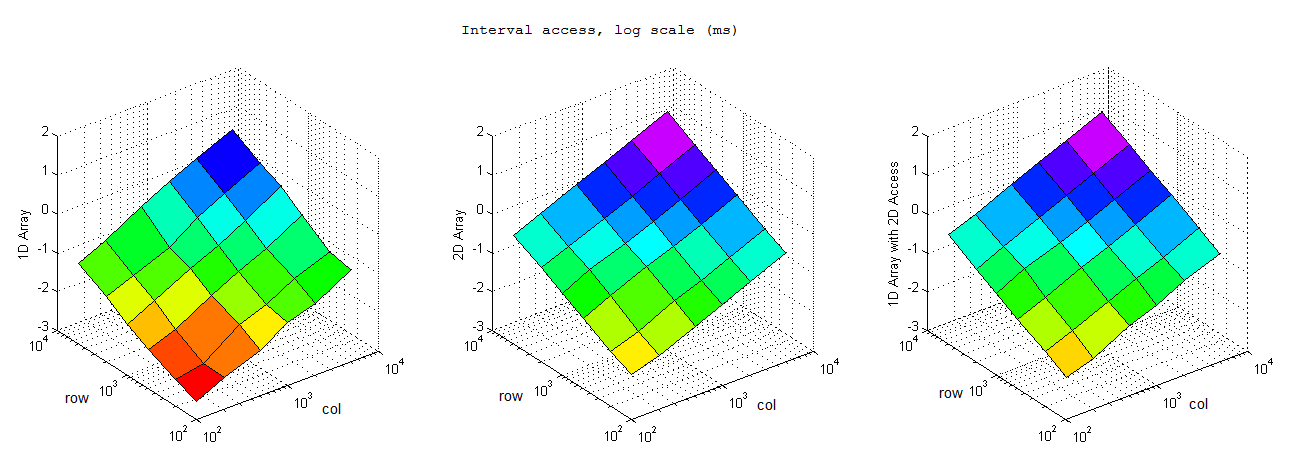
分析
內存的連續性:一維數組顯然有著比二維數組更好的連續性,我忘了以前是在哪看到的一個形象的字符畫說明一維數組和二維數組的區別,大概是下面這樣子:
一維數組:
┌--┬--┬--┬--┬- | | | | | ... └--┴--┴--┴--┴-
二維數組:
┌--┬--┬--┬--┬- | | | | | ... └--┴--┴--┴--┴- | | | | | V | | ┌--┬--┬--┬- | | | | | | ... | | └--┴--┴--┴- | V | ┌--┬--┬--┬--┬- | | | | | | ... | └--┴--┴--┴--┴- V ┌--┬--┬--┬--┬--┬- | | | | | | ... └--┴--┴--┴--┴--┴-
緩存命中率:緩存是SRAM,內存是DRAM,效率差很多,所以如果能提高緩存中的命中率,效率能提高很多。其實這和上一條其實也有關聯,顯然連續的內存命中率會高,不過如果申請的內存空間非常大那具體問題得具體分析了。
指令執行速度:由於早年體系沒學好,所以我也不知道這條有多大影響,另外現在的電腦都是多核的,作為不搞多核算法的人,不太懂會有多大影響。
對照結果可以看到基本上而言一維數組的效率完爆二維數組,尤其是內存申請和小內存訪問的情況,總體而言效率上一維數組>一維數組的二維引用>二維數組。不過也有比較有意思的發現:1) 逐行訪問的時候,在開辟內存空間小的時候一維數組二維索引效率高於二維數組,而大內存情況下卻變慢了。2) 逐列訪問基本符合預期,一維數組和一維數組二維索引效率接近,二維索引效率略低,但是都優於二維數組。3) 按間隔訪問的時候一維數組大幅快於逐行訪問,不太懂這是為什麼,是否我電腦是多核的影響?還是說VS的O2編譯的作用?
純屬蛋疼的測試,也相當不嚴謹,希望有體系知識比較豐富的大拿指點一二。
一維數組: 類型說明符 數組名[常量表達式]
例如 int a[10]它表示數組名為a,此數組有10個元素
二維數組: 數組名[下標][下標]
如 a[2][3] 下標可以是整形表達式如a[2-1][2*2-1]不能寫成a[2,3]
a[2-1,2*2-1]
假設 a[10][20]存放的是數,sum[10]存放每一行的和。
sum[10] = {0};
for( i =0; i < 10; i++)
for(j = 0; j < 20; j++)
sum[i] += a[i][j];