程式師世界 >> 編程語言 >> C語言 >> C++ >> C++入門知識 >> 關於二分查找及其上下界問題的一些思考，二分查找下界思考

關於二分查找及其上下界問題的一些思考，二分查找下界思考

編輯：C++入門知識

關於二分查找及其上下界問題的一些思考，二分查找下界思考

　　個人認為在編程的時候，我的代碼能力應該是到位的，但是昨天參加的某公司筆試徹底把這個想法給終結了，才意識到自己是多麼的弱。其中印象最深刻的是一道關於二分查找上下界的問題。當時洋洋得意，STL 分分鐘搞定，結果到了面試的時候他要我自己重新實現一下。這個時候就拙計了，拿著筆的我是寫了改改了寫，最後勉強算是完成。

　　今天反思一下，決定自己再把二分查找重新實現一下。也作為給自己的一個警醒，不要總以為自己能力有多高，總有一天會被打臉的。

一、二分查找思想（參照《算法競賽入門經典》，感謝劉老師）。

　　在有序表中查找元素常常使用二分查找（Binary Search），有時也譯為折半查找，它的基本思想就像是“猜數字游戲”：你在心裡想一個不超過1000的正整數，我可以保證在10次以內猜到它-----只要你每次告訴我猜的數比你想的大一些、小一些，或者正好猜中。

　　猜的方法就是二分。首先我猜500，除了運氣特別好正好猜中外，不管你說“太大”還是“太小”，我都可以把可行范圍縮小一半：如果“太大”，那麼答案在1~499之間，那我下一次猜250；如果“太小”，那麼答案在501~1000之間，那我下一次猜750。只要每次選擇可行區間的中間點去猜，每次都可以把范圍縮小一半。由於log₂1000 < 10，10次內一定能猜到。

二、STL二分查找

　　在STL中<algorithm>中已經有二分查找的實現了。我在這裡只給簡單的應用，也希望讀者多去了解一下STL的強大。下面的講解參照C++ Reference，有興趣看英文原文的戳鏈接。

　　1、binary_search()函數

　　　　該函數功能是查看某一值在一個已經排好序的序列中是否存在，當存在時返回true，否則返回false。其函數原型如下：

//default (1)    
template <class ForwardIterator, class T>
  bool binary_search (ForwardIterator first, ForwardIterator last,
                      const T& val);
//custom (2)    
template <class ForwardIterator, class T, class Compare>
  bool binary_search (ForwardIterator first, ForwardIterator last,
                      const T& val, Compare comp);

　　　　注意序列是迭代器表示，原則上可以代入多種數據類型。其中幾個參數如下：

　　　　first：序列需要查詢的開始位置；

　　　　last：序列需要查詢的結束位置；

　　　　val：需要查詢的元素；

　　　　comp：用戶自定義比較函數。

　　　　注意到default(1)和custom(2)的區別在於用戶有沒有自定義比較函數。對於default(1)版本，使用運算符 “<” 進行元素間的比較；對於custom(2)，使用用戶自定義comp進行元素間比較。

　　　　也就是說，binary_search()函數是在序列區間[first, last)中查找是否有某一元素。其中序列一定要先排好序，排序比較函數必須和二分查找比較函數相同。

　　2、lower_bound()函數

　　　　binary_search()只能告訴我們元素在序列中是否存在，卻無法定位它的確切位置。並且有時候所給的序列不一定是每個元素都不同的，同值的元素可能多次出現（因為已經排好序，所以相同的元素是相鄰的）。如果我們需要找到這些相同的元素中的第一個怎麼辦？

　　　　其實還STL中還定義了lower_bound()函數來解決這個問題，其函數原型如下：

//default (1)    
template <class ForwardIterator, class T>
  ForwardIterator lower_bound (ForwardIterator first, ForwardIterator last,
                               const T& val);
//custom (2)    
template <class ForwardIterator, class T, class Compare>
  ForwardIterator lower_bound (ForwardIterator first, ForwardIterator last,
                               const T& val, Compare comp);

　　這個函數的參數和binary_search()函數是相同的，我就不再贅述，但是它的返回類型是ForwardIterator，又見迭代器，為什麼不按照我們的要求返回一個整型值表示下表呢？這個我也不解，不過沒關系，我們照樣能得到我們想要的答案。

　　也就是說，這個函數的功能是返回迭代器的下界。

　　確切的說：如果所要查找的元素只有一個，那麼lower_lound()返回了這個元素的地址（注意這裡是地址，不是下標）；

　　　　　　如果所要查找的元素有多個相同，因為他們相鄰，所以可以用一個區間表示[first, last)（左閉右開）它們的位置，那麼lower_bound()函數返回的就是first的地

　　　　　　　址（再次強調是地址）。

　　3、upper_bound()函數

　　　　舉一反一，我們大概知道upper_bound()函數是干嘛的了吧，那就是返回迭代器上界，也就是所查找元素的區間的上界，但是和lower_bound()略有不同。

　　　　其函數原型如下：

//default (1)    
template <class ForwardIterator, class T>
  ForwardIterator upper_bound (ForwardIterator first, ForwardIterator last,
                               const T& val);
//custom (2)    
template <class ForwardIterator, class T, class Compare>
  ForwardIterator upper_bound (ForwardIterator first, ForwardIterator last,
                               const T& val, Compare comp);

　　　　注意我們之前有強調過，表示相同元素的區間[first, last)是左閉右開的，為什麼要這樣子？我不知道，你去問問寫這套STL的人吧，我不敢黑他。這就造成了lower_bound()和upper_bound()的一個不同之處。那就是：lower_bound()可以相等，upper_bound()不能相等。

　　　　更加詳細：如果元素只出現一次，那麼lower_bound()找到了這個元素的地址，但是upper_bound()找到的卻是它的下一個；

　　　　　　　　如果相同元素出現了多次，那麼lower_bound()找到了第一個所找元素的地址，但是upper_bound()找到的卻是最後一個元素的下一個元素的地址。

　　4、簡單例子測試。

　　　　知道上面的三個函數的使用方法了，那麼我們來具體操作一下：

　　　　測試代碼如下：

#include <iostream>
#include <cstdio>
#include <algorithm>
using namespace std;

int main()
{
    int a[] = {0, 0, 2, 2, 2, 4, 4, 4, 4, 5};
    int val;
    while(1)
    {
        printf("請輸入需要查找的數：");
        scanf("%d", &val);
        if(binary_search(a, a+10, val) == false)
            printf("未找到數 %d，請重新輸入!\n\n", val);
        else
        {
            printf("數 %d 已找到!\n", val);
            printf("相同個數： %d\n", upper_bound(a, a+10, val)-lower_bound(a, a+10, val));
            printf("下界為：   %d\n", lower_bound(a, a+10, val));
            printf("上界為：   %d\n\n", upper_bound(a, a+10, val));
        }
    }
    return 0;
}

　　當然上面的是三個函數最簡單的應用了，為了讓大家看得更清楚，讀者不要噴我一個函數寫了多次。我們可以查看所找元素是否存在，它第一次出現的位置和最後一次出現的位置，同時我們看知道了上下界就可以求出該元素出現了多少次。但是，我們看測試結果:

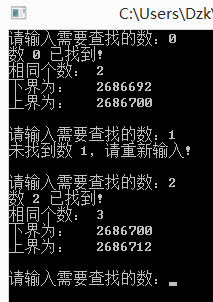
　　對，我們沒有看錯，這個上下界是地址。就拿2來看，上界減下界等於12，一個int型占用4個字節，那麼2的個數為3個。但是，我們要地址干什麼？沒有用啊！

　　別著急，想得到下標還不簡單。稍稍修改一下：

    printf("下界為：   %d\n", lower_bound(a, a+10, val)-a);     //減去首地址，就找到了下標位置
    printf("上界為：   %d\n", upper_bound(a, a+10, val)-a);   //同上
    printf("該元素所在范圍： [%d, %d)\n\n", lower_bound(a, a+10, val)-a, upper_bound(a, a+10, val)-a);

　　程序運行結果如圖：

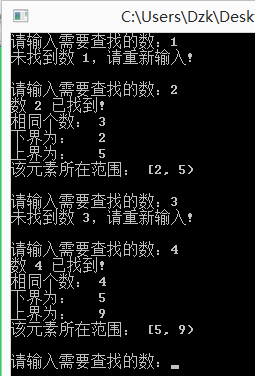
　　至此，STL二分查找的三個函數大致介紹完成，還有另外的幾個函數讀者有興趣可以上C++ Reference去挖掘一下。

三、手動實現二分查找三個函數。

　　本來今天的重點應該放在我是怎麼實現上的，不知道怎麼就跑偏了。其實講了思想，大家應該可以著手寫代碼了。不同人有不同人實現的方法，其中的技巧還是有不少的。下面給處我個人的實現，如果有人能挑出其中的缺陷，歡迎點評。

　　1、binary_search()函數

　　　　STL的binary_search()返回的是bool值，不過一般算法書或者數據結構書上都是這樣闡述的：若找到，輸出它的下標，若未找到，輸出-1。

　　　　下面呢，是我的簡單實現，功能如上所述：

#include <iostream>
#include <cstdio>
using namespace std;

int binary_search_1(int* A, int l, int r, int val)    //A為序列，l為左邊界，r為右邊界，val是元素
{
    //cout << l << " " << r << endl;
    if(l > r) return -1;                    //左邊界嚴格不大於右邊界，否則說明找不到
    int mid = l+(r-l)/2;                    //從中剖分，注意這裡的一個小技巧，為何不用(l+r)/2，讀者可以去思考,下面函數的注釋會給出解答。
    if(A[mid] == val) return mid;           //如果找到，返回
    if(A[mid] > val) r = mid-1;       //否則，修改邊界
    else l = mid+1;
    return binary_search_1(A, l, r, val);     //遞歸調用
}
int main()
{
    int a[] = {0, 0, 2, 2, 2, 4, 4, 4, 4, 5};
    cout << binary_search_1(a, 0, 10, 2);  //a為數組，0為起始位置，9為結束位置，表明你要查找的特定區間，現在為0~9，2為元素
    return 0;
}

　　　　下面看非遞歸版的：

int binary_search_2(int* A, int l, int r, int val)    //A為序列，l為左邊界，r為右邊界，val是元素
{
    int mid;
    while(l < r)
    {
        mid = l+(r-l)/2;
        if(A[mid] == val) return mid;
        if(A[mid] > val) r = mid-1;
        else l = mid+1;
    }
    return -1;
}

　　2、lower_bound()函數和upper_bound()函數

　　　　自己實現的binary_search()在元素都互不相同的時候還挺好，但是如果存在相同元素時，那就存在不確定性，那麼，它具體返回哪一個呢，這是不確定的。那麼我們來實現一下lower_bound()函數，求一下它的下界，既然是自己實現，就可以把下標輸出來了，規避掉地址。

　　代碼如下，參數與binary_search()相同：

#include <iostream>
#include <cstdio>
using namespace std;

int lower_bound_1(int* A, int l, int r, int val)    //二分求下界
{
    //cout << "l and r: " << l << " " << r << endl;
    if(l > r) return -1;
    if(A[l] == val) return l;
    int mid = l+(r-l)/2;         //注意這裡是l+(r-l)/2，當l+r是奇數時，mid它是更靠近l
    if(A[mid] > val) r = mid-1;
    else if( A[mid] == val) r = mid;
    else l = mid+1;
    return lower_bound_1(A, l, r, val);     //遞歸調用
}

int upper_bound_1(int* A, int l, int r, int val)    //二分求上界
{
    //cout << "l and r: " << l << " " << r << endl;
    if(l > r) return -1;
    if(A[r] == val) return r;
    int mid = l+(r-l+1)/2;      //注意這裡是l+(r-l+1)/2，當l+r是奇數時，mid它是更靠近r
    if(A[mid] > val) r = mid-1;
    else if( A[mid] == val) l = mid;
    else l = mid+1;
    return upper_bound_1(A, l, r, val);     //遞歸調用
}

int main()
{
    int a[] = {0, 0, 2, 2, 2, 4, 4, 4, 4, 5};
    printf("lower_bound at %d\n", lower_bound_1(a, 0, 9, 4));
    printf("upper_bound at %d\n", upper_bound_1(a, 0, 9, 4));
    return 0;
}

　　非遞歸代碼：

int lower_bound_2(int* A, int l, int r, int val) //非遞歸版本，參數設置三個函數都相同
{
    int mid;
    while(l < r)
    {
        mid = l+(r-l)/2;
        if(A[mid] > val) r = mid-1;
        else if(A[mid] == val) r = mid;
        else l = mid+1;
    }
    if(A[l] == val) return l;
    return -1;
}

int upper_bound_2(int* A, int l, int r, int val) //非遞歸版本，參數設置三個函數都相同
{
    int mid;
    while(l < r)
    {
        mid = l+(r-l+1)/2;
        if(A[mid] > val) r = mid-1;
        else if(A[mid] == val) l = mid;
        else l = mid+1;
    }
    if(A[r] == val) return r;
    return -1;
}

　　3、測試

　　　　自己已經在機器上測試了一遍，寫測試函數好累，讀者有興趣自己測試吧。偷個懶。

四、總結

　　二分查找的算法效率是非常非常高的，我相信我在這裡講的應該挺詳細了。下面有一道題就要用到二分的思想。

　　題目：

　　　　正整數數組a[0], a[1], a[2], ···, a[n-1]，n可以很大，大到1000000000以上，但是數組中每個數都不超過100。現在要你求所有數的和。假設這些數已經全部讀入內存，因而不用考慮讀取的時間。希望你用最快的方法得到答案。

　　提示：二分。

對於二分查找的問題

采用二分查找，比較的最大次數就是項數的一半，像樓主的問題，則最多比較250次

恩，樓主正解，應該是查找不成功的時候，才是比較次數最多的

二分查找對於ASL的問題

折半查找的asl可以畫出查找二叉樹來做：根節點是6，第二層是3、9，第三層是1、5、7、11，第四層是2、4、8、10、12；所以查找成功的話是是找到這些個節點，所以成功的asl=（1+2*2+3*4+4*4）/12=37 /12 而查找失敗的asl=（3*3+4*10）/13 =49/13
13是這個二叉樹的外部節點的個數