【注：相關概念來自經典教材、百度百科及維基百科】
樹狀圖是一種數據結構，它是由n（n>=1）個有限節點組成一個具有層次關系的集合。它具有以下的特點：
每個節點（node）有零個或多個子節點；沒有父節點的節點稱為根節點；每一個非根節點有且只有一個父節點；除了根節點外，每個子節點可以分為多個不相交的子樹；如圖所示：
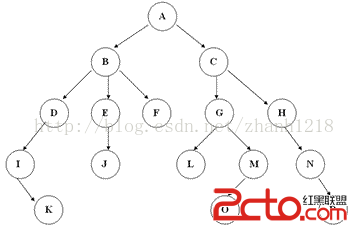
節點的度：一個節點含有的子樹的個數稱為該節點的度；樹的度：一棵樹中，最大的節點的度稱為樹的度；葉節點或終端節點：度為零的節點；非終端節點或分支節點：度不為零的節點；父親節點或父節點：若一個節點含有子節點，則這個節點稱為其子節點的父節點；孩子節點或子節點：一個節點含有的子樹的根節點稱為該節點的子節點；兄弟節點：具有相同父節點的節點互稱為兄弟節點；節點的層次：從根開始定義起，根為第1層，根的子節點為第2層，以此類推；樹的高度或深度：樹中節點的最大層次；堂兄弟節點：父節點在同一層的節點互為堂兄弟；節點的祖先：從根到該節點所經分支上的所有節點；子孫：以某節點為根的子樹中任一節點都稱為該節點的子孫。森林：由m（m>=0）棵互不相交的樹的集合稱為森林；
二叉樹的每個結點至多只有二棵子樹(不存在度大於2的結點)，二叉樹的子樹有左右之分，次序不能顛倒。二叉樹的第i層至多有
個結點；深度為k的二叉樹至多有
【用等比數列求和公式算算】個結點；對任何一棵二叉樹T，如果其終端結點數為
，度為2的結點數為
，則
。
樹和二叉樹的三個主要差別：
樹的結點個數至少為1，而二叉樹的結點個數可以為0；樹中結點的最大度數沒有限制，而二叉樹結點的最大度數為2；【度數即某節點的子節點個數】樹的結點無左、右之分，而二叉樹的結點有左、右之分。L、D、R分別表示遍歷左子樹、訪問根結點和遍歷右子樹。那麼根據排列組合，有6種可能。根據根的位置，常見以下三種遍歷方法。先中後是相對根節點說的。注：一定程度上維基百科授人與魚而不授人以漁，不能解惑。
先(根)序遍歷二叉樹的順序是DLR。【注意都是先L後R。】-----以下三張圖片來源於課件
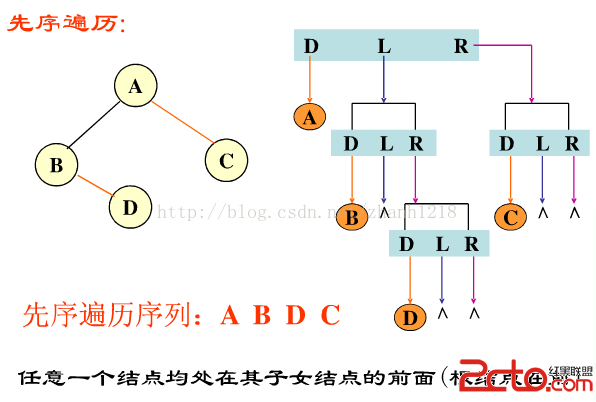
解釋：每個節點都用DLR的順序遍歷。下同。
中(根)序遍歷二叉樹的順序是LDR。【注意都是先L後R。】
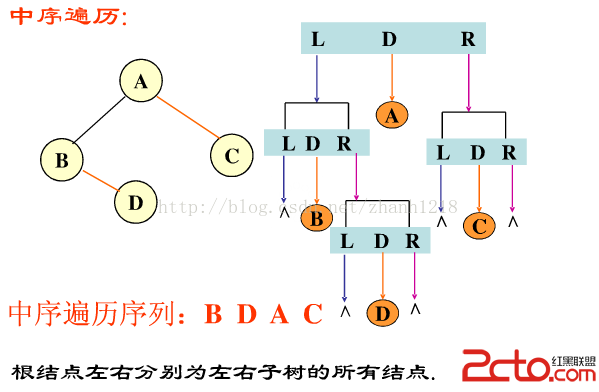
後(根)序遍歷二叉樹的順序是LRD。【注意都是先L後R。】
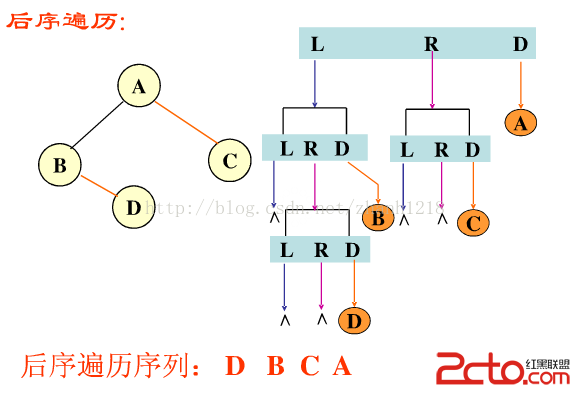
例子來源於互聯網及課件，分析為博主所寫，如有錯誤，懇請指正。
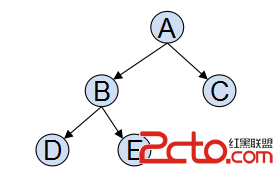
先序遍歷（根左右DLR）：ABDEC
中序遍歷（左根右LDR）：DBEAC
後序遍歷（左右根LRD）：DEBCA
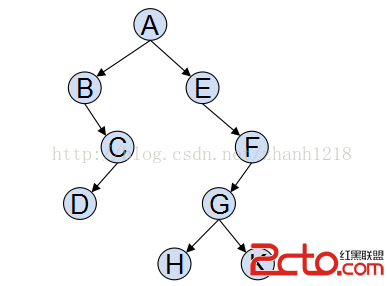
先序遍歷（根左右DLR）：ABCDEFGHK 【最簡單的。先把根寫下來，再寫左子樹的根，如果左子樹還有子樹，繼續往下找，直到葉子節點！因為根左右，先寫根，即遇到的就寫下來！只需要注意同層的先寫左，左如果有子樹，繼續遍歷其子樹。】
中序遍歷（左根右LDR）：BDCAEHGKF 【不好寫，容易犯錯。從左子樹開始尋找，子樹裡面還有子樹，繼續尋找其左子樹，直到遇到葉子節點（D）或者沒有左子樹（B）寫下來。例子裡B沒有左子樹，所以先寫，然後遍歷右子樹，右子樹也從其左子樹開始遍歷，所以是BCD；相對根節點，左子樹遍歷完成，所以是BDCA；接下來遍歷根節點的右子樹，按上述步驟，既是：E（其沒有左子樹）H（葉子節點，其沒有左子樹，且是G的L）G（自身為根D）K（相對於節點G，其為R）G（G為F的L）F】
後序遍歷（左右根LRD）：DCBHKGFEA 【先左子樹，再右子樹，最後根節點；沒有左子樹，則尋找此節點的右子樹，在右子樹裡再按照LRD的順序找，直到找到葉子節點（概念在上面），開始回溯寫下來，相當於堆棧！】
已知前序遍歷為GDAFEMHZ，中序遍歷為ADEFGHMZ，請畫出這棵二叉樹。
①根據前序遍歷特征，我們知道根結點必在首位置，所以為G；
②根據中序遍歷特征。其中根節點G左側的ADEF必然是根節點的左子樹，G右側的HMZ必然是根節點的右子樹；
③根據前序中序特征，重復以上步驟。遞歸找到子樹根節點；
那麼，我們可以畫出這個二叉樹：
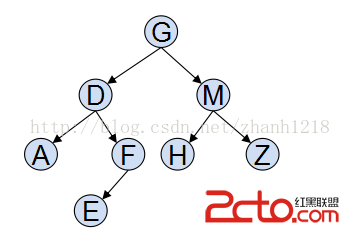
由圖可知，後序遍歷順序為：AEFDHZMG
已知一棵二叉樹的中序序列和後序序列分別是BDCEAFHG 和 DECBHGFA，請畫出這棵二叉樹。
分析：
①由後序遍歷特征，根結點必在後序序列尾部（即A）；
②由中序遍歷特征，根結點必在其中間，而且其左部必全部是左子樹的子孫（即BDCE），其右部必全部是右子樹的子孫（即FHG）；
③遞歸找出子樹根節點。
那麼，我們可以畫出這個二叉樹：
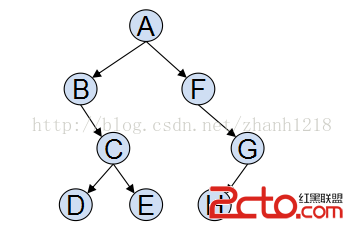
注意事項：
左子樹中序為BDCE，後序為DECB，說明B為A的左子樹根節點，C為B的右子樹（從BDCE看出）根節點（從DCE及DEC看出）；
右子樹中序為FHG，後序為HGF，說明F為A的右子樹的根節點，H為G的左子樹根節點。
