topcoder srm 623解題報告

topcoder srm 623解題報告

推薦使用插件greed 2.0，非常使用的插件。但我不知道如何自己添加測試數據，下次再學習下。
Greed 2.0 https://github.com/shivawu/topcoder-greed
250pt
題意：環形跑道上有n棵樹，標號為1--n，Alice跑步時記錄下一些樹的標號。問通過這些編號計算她最少跑了多少圈。
題解：稍微想一下就知道，一圈下來樹的編號都是遞增的，所以相鄰記錄非遞增則增加一圈，這樣圈數最少。

class RunningAroundPark {
    public:
    int numberOfLap(int N, vector d) {
      int cnt = 0;
      for(int i = 1; i < d.size(); i ++){
        if(d[i] <= d[i-1]) cnt ++;
      }
      return cnt+1;
    }
};

500pt
題意：有一序列未知a，但給一個序列d，其中d[i]表示a[i]換算為二進制時末尾零的個數。問a中存在多少對（i， j）使得i--j區間的數為幾何級數（等比數列，公比為實數）。
題解：考慮數位性質，a[i]與a[i+1]相差d[i+1]-d[i]個零，那麼a[i]左移或者右移d[i+1]-d[i]位得到a[i+1]，即乘以2^(d[i+1]-d[i])。所以區間(i, j)中d為等差數列，那麼a在相應的區間為等比數列。范圍不大，暴力。

class PotentialGeometricSequence {
    public:
    int numberOfSubsequences(vector d) {
      int cnt = 0;
      for(int l = 3; l <= d.size(); l ++){
        for(int i = 0; i <= d.size()-l; i ++){
            int g = d[i+1] - d[i];
            int flag = 1;
          for(int j = i+1; j < i+l-1; j ++){
            if(d[j+1]-d[j] != g) {flag = 0; break;}
           }
          if(flag == 1) cnt ++;
        }
      }
      return cnt+2*d.size()-1;
      // 2*d.size()-1分別是序列長度為1,2的時候的（i,j）對數
    }
};

1000 pt
題意：給定集合d,求有多少個d的子集，子集所有元素的積為goodValue。
題解：記憶化搜索。
注意事項：記憶化搜索因為是遞歸，所以要想清楚遞歸邊界，還有就是如果已存儲則直接返回不需要遞歸計算。

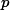
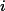
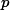
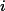
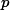
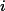
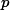
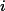
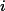
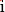
不整除 整除

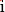
原諒我不會打整除和不整除符號，把公式弄殘了。還望大俠指教。

class GoodSubset {
    public:
    map, int> m;
    int dp(int goodValue, vector d, int cur){
      if(cur == 0){
        if(goodValue == 1) return 1;
        else return 0;
      }
      if(m.find(make_pair(goodValue, cur)) != m.end()){
        return m[make_pair(goodValue, cur)];
      }
      int ans = 0;
      if(goodValue%d[cur-1] != 0){
        return m[make_pair(goodValue, cur)] = dp(goodValue, d, cur-1);
      }else{
        ans += dp(goodValue, d, cur-1);
        ans %= mod;
        ans += dp(goodValue/d[cur-1], d, cur-1);
        ans %= mod;
        return m[make_pair(goodValue, cur)] = ans;
      }
    }
    int numberOfSubsets(int goodValue, vector d) {
      m.clear();
      int cnt = dp(goodValue, d, d.size());
      if(goodValue == 1) cnt --;
      return cnt;
    }
};