UVA - 1356 Bridge

UVA - 1356 Bridge

Description

A suspension bridge suspends the roadway from huge main cables, which extend from one end of the bridge to the other. These cables rest on top of high towers and are secured at each end by anchorages. The towers enable the main cables to be draped over long distances.

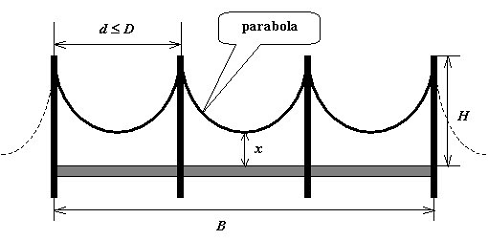
Suppose that the maximum distance between two neighboring towers is D , and that the distance from the top of a tower to the roadway isH . Also suppose that the shape of a cable between any two neighboring towers is the same symmetric parabola (as shown in the figure). Now givenB , the length of the bridge and L , the total length of the cables, you are asked to calculate the distance between the roadway and the lowest point of the cable, with minimum number of towers built (Assume that there are always two towers built at the two ends of a bridge).

Input

Standard input will contain multiple test cases. The first line of the input is a single integerT(1T10) which is the number of test cases. T test cases follow, each preceded by a single blank line.

For each test case, 4 positive integers are given on a single line.

D- the maximum distance between two neighboring towers; H- the distance from the top of a tower to the roadway; B- the length of the bridge; and L- the total length of the cables.

It is guaranteed that BL . The cable will always be above the roadway.

Output

Results should be directed to standard output. Start each case with "Case # : " on a single line, where # is the case number starting from 1. Two consecutive cases should be separated by a single blank line. No blank line should be produced after the last test case.

For each test case, print the distance between the roadway and the lowest point of the cable, as is described in the problem. The value must be accurate up to two decimal places.

Sample Input

2

20 101 400 4042

1 2 3 4

Sample Output

Case 1:
1.00

Case 2:
1.60
題意：修橋，橋上等距的擺放著若干個塔，塔高為H，相鄰兩座塔之間的距離不超過D，塔之間的繩索形成全等的對稱拋物線，橋長度為B，繩索長為L，問你繩索最下端離地的高度y。
思路間隔數為n=ceil(B/D)，每個間隔的寬度D1=B/n,每段的繩索長度為L1=L/n，然後根據D1和L1計算離地的高度，我們可以先求出一個拋物線，當開口寬度為w，高度為h的時候拋物線的長
來二分求解，這裡就需要高數的公式求可導函數的弧長了
#include 
#include 
#include 
#include 
#include 
using namespace std;

double F(double a, double x) {
	double a2 = a * a, x2 = x * x;
	return (x * sqrt(a2 + x2) + a2 * log(fabs(x + sqrt(a2 + x2)))) / 2;
}

double cal_length(double w, double h) {
	double a = 4.0 * h / (w * w);
	double b = 1.0 / (2 * a);
	return (F(b, w/2) - F(b, 0)) * 4 * a;
}

int main() {
	int t, cas = 1;
	scanf("%d", &t);
	while (t--) {
		int D, B, H, L;		
		scanf("%d%d%d%d", &D, &H, &B, &L);

		int n = (B + D - 1) / D;
		double D1 = (double) B / n;
		double L1 = (double) L / n;

		double x = 0, y = H;
		while (y - x > 1e-5) {
			double m = x + (y - x) / 2;
			if (cal_length(D1, m) < L1)
				x = m;
			else y = m;
		}

		if (cas > 1) printf("\n");
		printf("Case %d:\n%.2lf\n", cas++, H-x);
	}
	return 0;
}