摘要:本文討論了最長公共子串的的相關算法的時間復雜度,然後在後綴數組的基礎上提出了一個時間復雜度為o(n^2*logn),空間復雜度為o(n)的算法。該算法雖然不及動態規劃和後綴樹算法的復雜度低,但其重要的優勢在於可以編碼簡單,代碼易於理解,適合快速實現。
首先,來說明一下,LCS通常指的是公共最長子序列(Longest Common Subsequence,名稱來源參見《算法導論》原書第3版p223),而不是公共最長子串(也稱為最長公共子串)。
最長公共子串問題是在文本串、模式串中尋找共有的一個最長的子串,如文本串text=“abcbcedf”,pattern=“ebcbcdf”,則最長公共子串為“bcbc”,長度為4。
最長公共子串的解法很多,有蠻力搜索法、動態規劃法、後綴數組法、後綴樹法。本文著重提後綴數組法,其他方法可以自行百度。
蠻力搜索法
1 int enum_longestCommonSubstring(char *text,char *pattern)
2 {
3 if(!text || !pattern) return 0; //nullptr
4 int tlen=strlen(text),plen=strlen(pattern);
5 if(0==tlen || 0==plen) return 0; //empty string
6 int maxLEN=0,i=0,j=0,ofs=0;
7 for(i=0;i<tlen && (tlen-i>=maxLEN);++i)
8 for(j=0;j<plen && (plen-j>=maxLEN); ++j)
9 if( *(text+i)==*(pattern+j) )
10 {
11 ofs=1;
12 while((i+ofs)<tlen&&(j+ofs)<plen&&*(text+ofs)==*(pattern+ofs))
13 { ++ofs; }
14 if(ofs>maxLEN) maxLEN=ofs; //update
15 }
16 return maxLEN;
17 }
記文本串長度為m,模式串長度為n,則暴力搜索法時間復雜度為o(m*n*Min(m,n)),空間復雜度o(1)。在子串匹配問題上,如果使用KMP算法,則算法效率可以提高。
動態規劃
動態規劃求解最長公共子串問題的時間復雜度為o(m*n),經過優化後的動態規劃算法可以達到o(Min(m,n))的空間復雜度
參見http://www.cnblogs.com/ider/p/longest-common-substring-problem-optimization.html
後綴數組
利用排序後的後綴數組(suffix array)來求解最長公共子串步驟為:
一,拼接文本串和模式串得到一個新的串X;
二,將X的所有後綴數組存入sa;(文本串長度為m,模式串長n。步驟二時間復雜度o(m+n)
三,對sa進行排序;
四,計算sa中相鄰的子串的最長公共前綴長度(時間復雜度o((m+n)*Min(m,n)))
注:為了避免得到單個串的最長重復子串,在步驟四種參與比較的兩個子串應該為一個是文本串的子串,另一個為模式串的子串。因此,在步驟一、二中就應該附加記錄位來處理。
《後綴數組——————處理字符串的有力工具處理字符串的有力工具》羅穗骞介紹了使用基數排序來排序後綴數組的方法,排序時間復雜度(m+n)*log(m+n)。因此,使用使用後綴數組+基數排序得到的算法的時間復雜度為o((m+n)*Min(m,n))(步驟四決定最大時間復雜度)。但是,該方法較復雜,不容易掌握,在此處,我提出一種後綴數組+C標准庫sort排序的算法,其排序時間復雜度為o(Min(m,n)*(m+n)*log(m+n)),因此,算法整體的時間復雜度為o(Min(m,n)*(m+n)*log(m+n))(由步驟三決定最大時間復雜度),此外,該算法空間復雜度為o(m+n)。 “後綴數組+快排”算法時間復雜低於“後綴數組+基數排序”的時間復雜度,但優點在於利用標准庫sort+strcmp來實現排序,代碼簡單,算法更容易理解。代碼如下:
1 #include<stdio.h>
2 #include<iostream>
3 #include<string.h>
4 #include<algorithm>
5 using namesapce std;
6 int suffixArrayQsort_longestCommonSubstring(char *text,char *pattern)
7 {
8 if(!text || !pattern) return 0; //nullptr
9 int tlen=strlen(text),plen=strlen(pattern),i,j;
10 if(0==tlen || 0==plen) return 0; //empty string
11
12 enum ATTRIB{TEXT,PATTERN};
13 struct absInfo
14 {
15 char *head;
16 ATTRIB attr; //tag
17 int len;
18 absInfo():head(NULL),attr(TEXT),len(0){}
19 absInfo(char *phead,ATTRIB attrib,int length):head(phead),attr(attrib),len(length){}
20 bool operator < (const absInfo &b)
21 {
22 return strcmp(head,b.head)<0;
23 }
24 static void display(const absInfo &a)
25 {
26 printf("size:%d type:%-7s ",a.len, (a.attr==TEXT?"TEXT":"PATTERN") );
27 printf("%s\n",a.head);
28 }
29 }*sa;
30
31 //step 2:build the suffix array
32 sa=new absInfo[tlen+plen];
33 for(i=0;i<tlen;++i)
34 {
35 sa[i].head=text+i;
36 sa[i].attr=TEXT;
37 sa[i].len=tlen-i;
38 }
39 for(j=0;j<plen;++j)
40 {
41 sa[j+tlen].head=pattern+j;
42 sa[j+tlen].attr=PATTERN;
43 sa[j+tlen].len=plen-j;
44 }
45
46 //step 3:use sort() to sort the sa
47 puts("before sort, the sa is:"); for_each(sa,sa+tlen+plen,absInfo::display);
48 sort(sa,sa+tlen+plen);
49 puts("after sort, the sa is:"); for_each(sa,sa+tlen+plen,absInfo::display);
50
51 //step 4:compare
52 int maxLEN=0,rec=0;
53 for(i=0;i<tlen+plen-1;i++)
54 {
55 if(sa[i].attr==sa[i+1].attr) continue;
56 if(sa[i].len<=maxLEN || sa[i+1].len<=maxLEN) continue;
57 rec=0;
58 while(rec<sa[i].len && rec<sa[i+1].len && *(sa[i].head+rec)==*(sa[i+1].head+rec) )
59 ++rec;
60 if(rec>maxLEN) maxLEN=rec; //update
61 }
62 //release memory resource and return
63 delete [] sa; sa=NULL;
64 return maxLEN;
65 }
注:1,absInfo結構中len字段不是必須的,設置此字段只是為了在代碼56行處做一個搜索剪枝操作。
2,稍微改動代碼就能在算法中給出公共子串的值(對示例來說就是給出“bcbc"),通過absInfo的len字段和maxLEN值也可以在o(1)的時間復雜度內計算出公共子串分別在文本串和模式串中的位置
運行結果:
當文本串text=“abcbcedf”,pattern=“ebcbcdf”時,代碼運行如下圖所示:
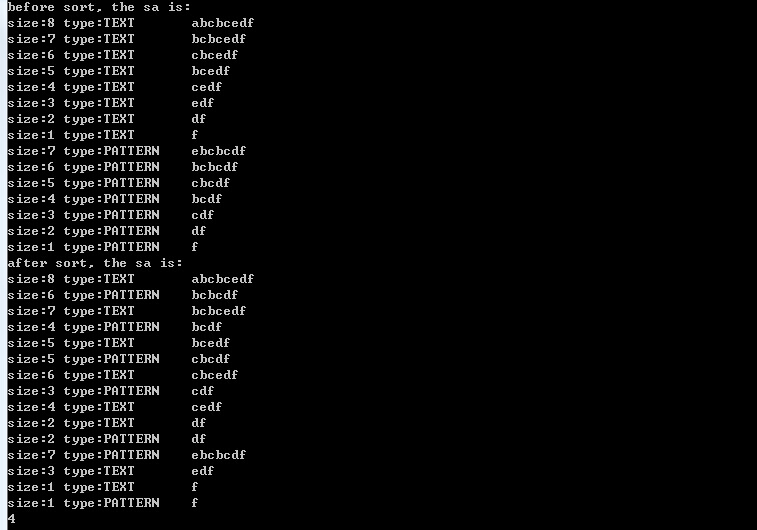
從代碼可以看出,“後綴數組+qsort排序”實現最長公共子串具有編碼簡單的特點,空間復雜度為o(m+n)
後綴樹
後綴樹以及廣義的後綴樹算法讀者可以自行搜索。
因為不加 就搞不清楚到底哪一部分是屬於第一個字符串,哪一部分是屬於第2個字符串...這樣談何求幾個字符串的公共子串
後綴數組
在字符串處理當中,後綴樹和後綴數組都是非常有力的工具,其中後綴樹大家了解得比較多,關於後綴數組則很少見於國內的資料。其實後綴數組是後綴樹的一個非常精巧的替代品,它比後綴樹容易編程實現,能夠實現後綴樹的很多功能而時間復雜度也不太遜色,並且,它比後綴樹所占用的空間小很多。可以說,在信息學競賽中後綴數組比後綴樹要更為實用。因此在本文中筆者想介紹一下後綴數組的基本概念、構造方法,以及配合後綴數組的最長公共前綴數組的構造方法,最後結合一些例子談談後綴數組的應用。
基本概念
首先明確一些必要的定義:
字符集 一個字符集∑是一個建立了全序關系的集合,也就是說,∑中的任意兩個不同的元素α和β都可以比較大小,要麼α<β,要麼β<α(也就是α>β)。字符集∑中的元素稱為字符。
字符串 一個字符串S是將n個字符順次排列形成的數組,n稱為S的長度,表示為len(S)。S的第i個字符表示為S。
子串 字符串S的子串S[i..j],i≤j,表示S串中從i到j這一段,也就是順次排列S,S[i+1],...,S[j]形成的字符串。
後綴 後綴是指從某個位置i開始到整個串末尾結束的一個特殊子串。字符串S的從i開頭的後綴表示為Suffix(S,i),也就是Suffix(S,i)=S[i..len(S)]。
關於字符串的大小比較,是指通常所說的“字典順序”比較,也就是對於兩個字符串u、v,令i從1開始順次比較u和v,如果相等則令i加1,否則若u<v則認為u<v,u>v則認為u>v(也就是v<u),比較結束。如果i>len(u)或者i>len(v)仍未比較出結果,那麼若len(u)<len(v)則認為u<v,若len(u)=len(v)則認為u=v,若len(u)>len(v)則u>v。
從字符串的大小比較的定義來看,S的兩個開頭位置不同的後綴u和v進行比較的結果不可能是相等,因為u=v的必要條件len(u)=len(v)在這裡不可能滿足。
下面我們約定一個字符集∑和一個字符串S,設len(S)=n,且S[n]='$',也就是說S以一個特殊字符'$'結尾,並且'$'小於∑中的任何一個字符。除了S[n]之外,S中的其他字符都屬於∑。對於約定的字符串S,從位置i開頭的後綴直接寫成Suffix(i),省去參數S。
後綴數組 後綴數組SA是一個一維數組,它保存1..n的某個排列SA[1],SA[2],...SA[n],並且保證 Suffix(SA)<Suffix(SA[i+1]),1≤i<n。也就是將S的n個後綴從小到大進行排序之後把排好序的後綴的開頭位置順次放入SA中。
名次數組 名次數組Rank=SA-1,也就是說若SA=j,則Rank[j]=i,不難看出Rank保存的是Suffix(i)在所有後綴中從小到大排列的“名次”。
構造方法
如何構造後綴數組呢?最直接最簡單的方法當然是把S的後綴都看作一些普通的字符串,按照一般字符串排序的方法對它們從小到大進行排序。
不難看出,這種做法是很笨拙的,因為它沒有利用到各個後綴之間的有機聯系,所以它的效率不可能很高。即使采用字符串排序中比較高效的Multi-key Quick Sort,最壞情況的時間復雜度仍然是O(n2)的,不能滿足我們的需要。
下面介紹倍增算法(Doubling Algorithm),它正......余下全文>>